
分析 (1)根据每天所获利润=甲种零件所获利润+乙种零件所获利润,可列出函数关系式;
(2)根据车间每天所获利润不低于49000元,可列出不等式.
解答 解:(1)根据题意,可得y=150×6x+260×5(20-x)=-400x+26000(0≤x≤20);
(2)由题意可知:400×6x+500×5(20-x)≤49000,
解得:x≥10,
由于甲种零件的利润低,乙种零件的利润高,
所以甲种零件制造的越少,乙种零件制造的越多厂家每天的利润才会越大,
最大利润为:10×6×150+10×5×260=22000(元).
点评 本题主要考查了一次函数的应用,正确得出找出各个量之间的关系式,列出函数关系式或不等式是解题关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
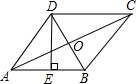 如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )| A. | ①②④⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
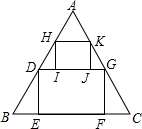 如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.
如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
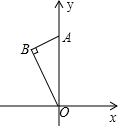 如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )
如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com