练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．当x=-6时，代数式$\frac{1}{4}$（3x-2）与-x-1互为相反数．

    分析 利用互为相反数两数之和为0列出方程，求出方程的解即可得到x的值．

    解答 解：根据题意得：$\frac{1}{4}$（3x-2）+（-x-1）=0，
    去分母得：3x-2+4（-x-1）=0，
    去括号得：3x-2-4x-4=0
    移项合并得：-x=6，
    系数化为1得：得x=-6．
    故答案为：-6．

    点评 本题考查的是解一元一次方程、相反数的定义，根据相反数的定义得出关于x的一元一次方程是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．为加强我县创建文明卫生县城宣传力度，需要在甲楼A处到E处悬挂一幅宣传条幅，在乙楼顶部D点测得条幅顶端A点的仰角为45°，条幅底端E点的仰角为30°，若甲、乙两楼的水平距离BC为21米，求条幅的长约是多少米？（结果精确到0.1米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若2a=3b，则$\frac{2{a}^{2}}{3{b}^{2}}$的值是（　　）
    A．1B．$\frac{2}{3}$C．$\frac{3}{2}$D．$\frac{9}{6}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

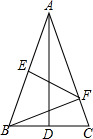    7．如图，△ABC，AB=AC，AD为△ABC的角平分线，过AB的中点E作AB的垂线交AC于点F，连接BF，若AB=5，CD=2，则△BFC的周长为（　　）
    A．7B．9C．12D．14

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

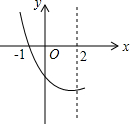    14．如图，是抛物线y=ax2+bx+c（a≠0）的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（-1，0），则方程ax2+bx+c=0（a≠0）的两根是x1=-1，x2=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

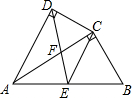    4．如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点．连接CE，连接DE交AC于F，AD=4，AB=6．
    （1）求证：△ADC∽△ACB；
    （2）求AC的值；
    （3）求$\frac{AC}{AF}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在Rt△ACB中，∠C=90°，AC=30cm，BC=25cm，动点P从点C出发，沿CA方向运动，速度是2cm/s，动点Q从点B出发，沿BC方向运动，速度是1cm/s．
    （1）几秒后P、Q两点相距25cm？
    （2）几秒后△PCQ与△ABC相似？
    （3）设△CPQ的面积为S1，△ABC的面积为S2，在运动过程中是否存在某一时刻t，使得S1：S2=2：5？若存在，求出t的值；若不存在，则说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．一个正方体的6个面分別标有“E”、“F”、“G”、“H”、“M”、“N”中的一个字母，如图表示的是该正
    方体3种不同的摆法，当“E”在右面时，左面的字母是（　　）
    A．GB．HC．MD．N

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在△ABC中，画出：
    （1）∠C的平分线CD；
    （2）边AC上的中线BM；
    （3）边BC上的高AH．

    查看答案和解析>>

    同步练习册答案