
 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB、AC
如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB、AC分析 (1)直接利用三角形的内角和球的答案即可;
(2)根据三角形的内角和等于180°求出∠ADE+∠AED,再根据翻折变换的性质可得∠NDE=∠ADE,∠NED=∠AED,然后利用平角等于180°列式计算即可得解.
解答 解:(1)∠A=180°-∠B-∠C=180°-35°-60°=85°;
(2)∵∠A=70°,
∴∠ADE+∠AED=180°-70°=110°,
∵△ABC沿着DE折叠压平,A与N重合,
∴∠NDE=∠ADE,∠NED=∠AED,
∴∠1+∠2=180°-(∠NED+∠AED)+180°-(∠NDE+∠ADE)=360°-2×110°=140°.
故答案为:85°,140°.
点评 本题考查了三角形的内角和定理,翻折变换的性质,平角的意义,渗透整体思想的利用,掌握三角形的内角和180°是解决问题的关键.


科目:初中数学 来源: 题型:解答题
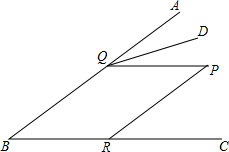 如图,点P在∠ABC内,点Q,R分别在∠ABC的边BA,BC上,QD平分∠AQP,连接PQ,PR.若∠PRC=∠B,∠P=50°,求∠PQD的度数.
如图,点P在∠ABC内,点Q,R分别在∠ABC的边BA,BC上,QD平分∠AQP,连接PQ,PR.若∠PRC=∠B,∠P=50°,求∠PQD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
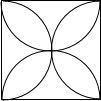 分别以正方形的各边为直径向其内部作半圆得到的图形如图所示,将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是( )
分别以正方形的各边为直径向其内部作半圆得到的图形如图所示,将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是( )| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 保持不变 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com