
【题目】已知二次函数![]() (
(![]() 、
、![]() 为常数)的图像经过点
为常数)的图像经过点![]() 和点
和点![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
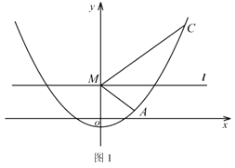
(2)如图1,点![]() 在抛物线上,点
在抛物线上,点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 平分
平分![]() ,求点
,求点![]() 的坐标;
的坐标;
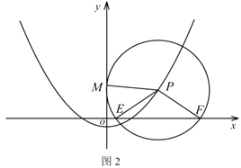
(3)如图2,在(2)的条件下,点![]() 是抛物线上的一动点,以
是抛物线上的一动点,以![]() 为圆心、
为圆心、![]() 为半径的圆与
为半径的圆与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)直接把两点的坐标代入二次函数解析式,得出关于b,c的二元一次方程组求解即可
(2) 过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .证明△CMD相似于△AME,再根据对应线段成比例求解即可
.证明△CMD相似于△AME,再根据对应线段成比例求解即可
(3)根据题意设点P的纵坐标为y,首先根据三角形面积得出EF与y的关系,再利用勾股定理得出EF与y的关系,从而得出y的值,再代入抛物线解析式求出x的值,得出点坐标.
解:(1)把![]() 和
和![]() 代入
代入![]() 得:
得:![]()
解方程组得出:![]()
所以,
![]() ,
,![]()
(2)由已知条件得出C点坐标为![]() ,设
,设![]() .过点
.过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .
.
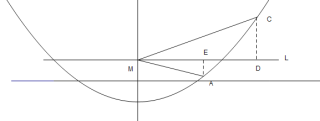
两个直角三角形的三个角对应相等,
∴![]()
∴![]()
∴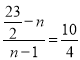
∵解得:![]()
∴![]()
(3)设点P的纵坐标为y,由题意得出,![]() ,
,![]()
∵MP与PE都为圆的半径,
∴MP=PE
∴![]()
整理得出,
∴![]()
∵![]()
∴y=![]() 1,
1,
∴当y=1时有,![]() ,解得,
,解得,![]() ;
;
∴当y=-1时有,![]() ,此时,x=0
,此时,x=0
∴综上所述得出P的坐标为:![]() 或
或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.

(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下社团:A.足球、B.机器人、C.航模、D.绘画,学校要求每人只能参加一个社团小丽和小亮准备随机报名一个项目.
(1)求小亮选择“机器人”社团的概率为______;
(2)请用树状图或列表法求两人至少有一人参加“航模”社团的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点.
边上的动点.

(1)连接![]() 、
、![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() .
.
①若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②若![]() ,求
,求![]() 的长;
的长;
(2)已知![]() ,
,![]() ,
,![]() 是以
是以![]() 为弦的圆.
为弦的圆.
①若圆心![]() 恰好在
恰好在![]() 边的延长线上,求
边的延长线上,求![]() 的半径:
的半径:
②若![]() 与矩形
与矩形![]() 的一边相切,求
的一边相切,求![]() 的半径.
的半径.
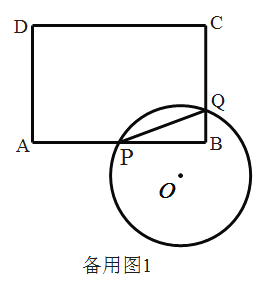
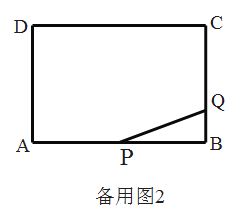
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+1﹣2k(k≠0)的图象记作G1,一次函数y2=2x+3(﹣1<x<2)的图象记作G2,对于这两个图象,有以下几种说法:
①当G1与G2有公共点时,y1随x增大而减小;
②当G1与G2没有公共点时,y1随x增大而增大;
③当k=2时,G1与G2平行,且平行线之间的距离为![]() .
.
下列选项中,描述准确的是( )
A.①②正确,③错误B.①③正确,②错误
C.②③正确,①错误D.①②③都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一个动点(不与
上一个动点(不与![]() 、
、![]() 重合),点
重合),点![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,设
,设![]() .
.
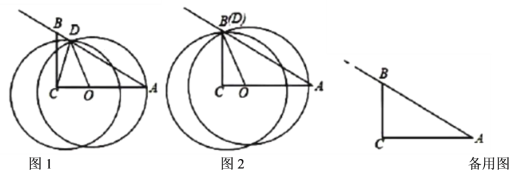
(1)如图2,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)当点![]() 在线段
在线段![]() 上,如果
上,如果![]() 与
与![]() 的另一个交点
的另一个交点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,试求
,试求![]() 与
与![]() 之间的函数解析式,并写出
之间的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)在点![]() 的运动过程中,如果
的运动过程中,如果![]() 与线段
与线段![]() 只有一个公共点,请直接写出
只有一个公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com