
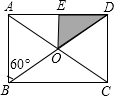
 小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游戏(每次飞镖均落在纸板上),击中阴影区域的概率是$\frac{1}{8}$.
小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游戏(每次飞镖均落在纸板上),击中阴影区域的概率是$\frac{1}{8}$. 科目:初中数学 来源: 题型:选择题
| A. | 22 | B. | 24 | C. | 16 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
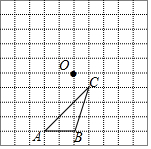 如图所示,△ABC与点O在10×10的网格中的位置如图所示,设每个小正方形的边长为1.
如图所示,△ABC与点O在10×10的网格中的位置如图所示,设每个小正方形的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
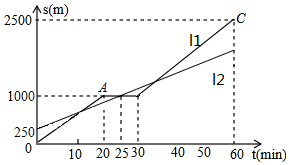 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com