
分析 (1)设剪成的较短的这段为xcm,较长的这段就为(40-x)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于58cm2建立方程求出其解即可;
(2)设剪成的较短的这段为mcm,较长的这段就为(40-m)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于48cm2建立方程,如果方程有解就说明李明的说法错误,否则正确.
解答 解:(1)设剪成的较短的这段为xcm,较长的这段就为(40-x)cm,由题意,得
($\frac{x}{4}$)2+($\frac{40-x}{4}$)2=58,
解得:x1=12,x2=28,
当x=12时,较长的为40-12=28cm,
当x=28时,较长的为40-28=12<28(舍去).
答:李明应该把铁丝剪成12cm和28cm的两段;
(2)李明的说法正确.理由如下:
设剪成的较短的这段为mcm,较长的这段就为(40-m)cm,由题意,得
($\frac{m}{4}$)2+($\frac{40-m}{4}$)2=48,
变形为:m2-40m+416=0,
∵△=(-40)2-4×416=-64<0,
∴原方程无实数根,
∴李明的说法正确,这两个正方形的面积之和不可能等于48cm2.
点评 本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,根的判别式的运用,解答本题时找到等量关系建立方程和运用根的判别式是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
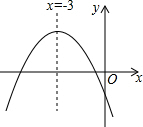 二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )
二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )| A. | y1<y3<y2 | B. | y1>y2>y3 | C. | y3<y2=y1 | D. | y1=y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
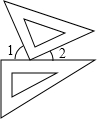 一副三角板按如图方式摆放,且∠1比∠2大50°.若设∠1=x°,∠2=y°,则可得到的方程组为( )
一副三角板按如图方式摆放,且∠1比∠2大50°.若设∠1=x°,∠2=y°,则可得到的方程组为( )| A. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=180}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=180}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=90}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=90}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com