
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
![]() 将函数关系式用配方法化为
将函数关系式用配方法化为![]() 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
![]() 在直角坐标系中,画出它的图象.
在直角坐标系中,画出它的图象.
![]() 根据图象说明:当
根据图象说明:当![]() 取何值时,
取何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 当
当![]() 取何值时,
取何值时,![]() ?
?

【答案】(1)![]() ,它的顶点坐标为
,它的顶点坐标为![]() 、对称轴为:
、对称轴为:![]() ;
;![]() 画图象见解析;
画图象见解析;![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 时,
时,![]() .
.
【解析】
(1)用配方法整理,进而得出顶点坐标和对称轴即可;
(2)让函数值为0,求得一元二次方程的两个解即为这个二次函数的图象与坐标轴的交点的横坐标,让x=0,可求得抛物线与y轴的交点坐标;
找到与y轴的交点,x轴的交点,对称轴,即可画出大致图象;
(3)根据对称轴为x=2,结合图象开口方向,即可得出答案;
(4)找到x轴上方函数图象所对应的自变量的取值即可.
解:(1)![]() ;
;
故它的顶点坐标为![]() 、对称轴为:
、对称轴为:![]() ;
;
![]() 图象与
图象与![]() 轴相交是
轴相交是![]() ,则:
,则:
![]() ,
,
解得![]() ,
,![]() ,
,
∴这个二次函数的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,
∴与![]() 轴的交点坐标为
轴的交点坐标为![]() ;
;
画出大致图象为:
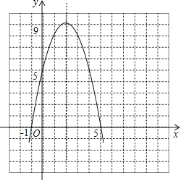 ;
;
![]() 根据图象对称轴为
根据图象对称轴为![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
![]() 由图中可以看出,当
由图中可以看出,当![]() 时,
时,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).
(1)直接写出![]() 的坐标 ; (用
的坐标 ; (用![]() 的代数式表示)
的代数式表示)
(2)设抛物线的顶点为![]() ,对称轴
,对称轴![]() 与直线
与直线![]() 的交点为
的交点为![]() ,连结
,连结![]() 、
、![]() ,若S△NDC=3×S△MDC,求抛物线的解析式;
,若S△NDC=3×S△MDC,求抛物线的解析式;
(3)如图②,在(2)的条件下,设该抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 为直线
为直线![]() 下方抛物线上一动点,连接
下方抛物线上一动点,连接![]() 、
、![]() ,设直线
,设直线![]() 交线段
交线段![]() 于点
于点![]() ,△MPQ的面积为
,△MPQ的面积为![]() ,△MAQ的面积为
,△MAQ的面积为![]() ,求
,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
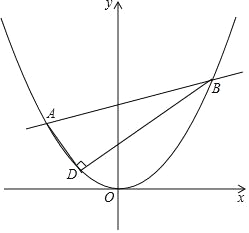
【题目】已知抛物线y=![]() x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
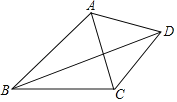
【题目】如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=74°,∠ABC=46°,且∠BAD+∠CAD=180°,那么∠BDC的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD为△ABC的中线,点E在CD上,且∠AED=∠BCD.

(1)求证:AE=BC.
(2)如图2,连接BE,若AB=AC=2DE,∠CBE=14°,则∠ACD的度数为 (直接写出结果),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(其中
两点(其中![]() 为坐标原点),过点
为坐标原点),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() (其中
(其中![]() 、
、![]() 不重合),连接
不重合),连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 和
和![]() .
.
(1)![]() 时,求抛物线的解析式和
时,求抛物线的解析式和![]() 的长;
的长;
![]() 如图
如图![]() 时,若
时,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高为![]() 米的小区超市,超市以上是居民住房,现计划在该楼前面
米的小区超市,超市以上是居民住房,现计划在该楼前面![]() 米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为
米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为![]() .(参考数据在
.(参考数据在![]() ,
,![]() )
)
![]() 中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
![]() 若新建的大楼高
若新建的大楼高![]() 米,则中午时,超市以上的居民住房采光是否受影响,为什么?
米,则中午时,超市以上的居民住房采光是否受影响,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图1和图2中的四边形ABCD都是正方形,△ABE的边长分别为a,b,c,请你从图1到图2,图2到图3的变换过程中,利用几何图形的面积关系,求a,b,c之间的等量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
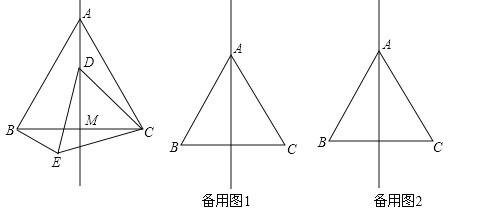
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com