
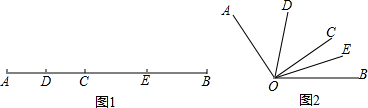
分析 (1)根据中点的性质求出AC、BC的长,根据线段中点的定义计算即可;
(2)根据中点的性质求出AC、BC的长,根据线段中点的定义计算即可;
(3)根据中点的性质求出AC、BC的长,根据线段中点的定义计算即可说明结论;
(4)根据角平分线的定义得到∠DOC=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}∠$BOC,结合图形计算即可.
解答 解:(1)∵点C恰为AB的中点,
∴AC=BC=$\frac{1}{2}$AB=8cm,
∵点D、E分别是AC和BC的中点,
∴DC=$\frac{1}{2}$AC=4cm,CE=$\frac{1}{2}$BC=4cm,
∴DE=8cm;
(2)∵AB=16cm,AC=6cm,
∴BC=10cm,
由(1)得,DC=$\frac{1}{2}$AC=3cm,CE=$\frac{1}{2}$CB=5cm,
∴DE=8cm;
(3)∵点D、E分别是AC和BC的中点,
∴DC=$\frac{1}{2}$AC,CE=$\frac{1}{2}$BC,
∴DE=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB,
∴不论AC取何值(不超过16cm),DE的长不变;
(4)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}∠$BOC,
∴∠DOE=∠DOC+∠EOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=65°,
∴∠DOE=65°与射线OC的位置无关.
点评 本题考查的是两点间的距离的计算和角的计算,掌握线段中点的定义、角平分线的定义、灵活运用数形结合思想是解题的关键.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:选择题
| A. | 3.241×103 | B. | 0.3241×104 | C. | 3.241×1011 | D. | 3.241×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
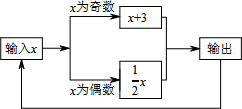 有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2016次输出的结果是2.
有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2016次输出的结果是2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
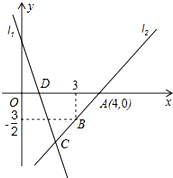 如图,直线l1的表达式为y=-3x+3,且直线l1与x轴交与点D,直线l2经过点A、B,且与直线l1交于点C,则△BDC的面积为$\frac{9}{4}$.
如图,直线l1的表达式为y=-3x+3,且直线l1与x轴交与点D,直线l2经过点A、B,且与直线l1交于点C,则△BDC的面积为$\frac{9}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com