
【题目】如图1是小区常见的漫步机,从侧面看如图2,踏板静止时,踏板连杆与立柱![]() 上的线段
上的线段![]() 重合,
重合,![]() 长为0.2米,当踏板连杆绕着点
长为0.2米,当踏板连杆绕着点![]() 旋转到
旋转到![]() 处时,测得
处时,测得![]() ,此时点
,此时点![]() 距离地面的高度
距离地面的高度![]() 为0.44米.求:
为0.44米.求:

(1)踏板连杆![]() 的长.
的长.
(2)此时点![]() 到立柱
到立柱![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)1.2米 (2)0.72米
【解析】
(1)过点C作CG⊥AB于G,得到四边形CFEG是矩形,根据矩形的性质得到EG=CF=0.44,故BG=0.24设AG=x,求得AB=x+0.24,AC=AB=x+0.24,根据余弦的定义列方程即可求出x,即可求出AB的长;
(2)利用正弦即可求出CG的长.
(1)过点C作CG⊥AB于G,
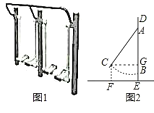
则四边形CFEG是矩形,
∴EG=CF=0.44,
故BG=0.24
设AG=x,
∴AB=x+0.24,AC=AB=x+0.24,
在Rt△ACG中,∠AGC=90°,∠CAG=37°,
cos∠CAG=![]() =0.8,
=0.8,
解得:x=0.96,
经检验,x=0.96符合题意,
∴AB=x+0.24=1.2(米),
(2)点![]() 到立柱
到立柱![]() 的距离为CG,
的距离为CG,
故CG=ACsin37°=1.2×0.6=0.72(米)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
科目:初中数学 来源: 题型:
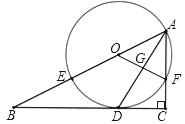
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
![]() 他们在一次实验中共掷骰子
他们在一次实验中共掷骰子![]() 次,试验的结果如下:
次,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最大.”她的说法正确吗?为什么?
点朝上的概率最大.”她的说法正确吗?为什么?
![]() 小颖和小红在实验中如果各掷一枚骰子,那么枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
小颖和小红在实验中如果各掷一枚骰子,那么枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
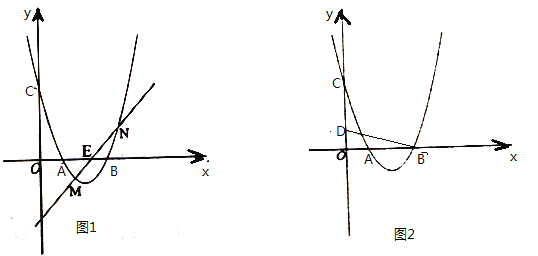
(1)填空:![]() ,
,![]() .
.
(2)如图1,已知![]() ,过点
,过点![]() 的直线与抛物线交于点
的直线与抛物线交于点![]() 、
、![]() ,且点
,且点![]() 、
、![]() 关于点
关于点![]() 对称,求直线
对称,求直线![]() 的解析式.
的解析式.
(3)如图2,已知![]() ,
,![]() 是第一象限内抛物线上一点,作
是第一象限内抛物线上一点,作![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 相似,请求出点
相似,请求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 为抛物线的顶点,
为抛物线的顶点,![]() 为线段
为线段![]() 中点.
中点.
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)以抛物线的顶点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 是圆上一动点,点
是圆上一动点,点![]() 为
为![]() 的中点(如图2);
的中点(如图2);
①当![]() 面积最大时,求
面积最大时,求![]() 的长度;
的长度;
②若点![]() 为
为![]() 的中点,求点
的中点,求点![]() 运动的路径长.
运动的路径长.
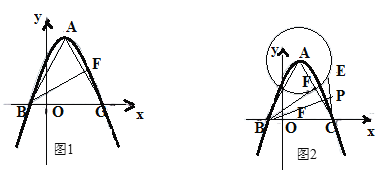
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种成本为10元的产品,经市场调查发现,在一段时间内,销售量![]() (件)与销售单价
(件)与销售单价![]() ( 元/件 )的关系如下表:
( 元/件 )的关系如下表:
|
| 15 | 20 | 25 | 30 |
|
|
| 550 | 500 | 450 | 400 |
|
设这种产品在这段时间内的销售利润为![]() (元),解答下列问题:
(元),解答下列问题:
(1)如![]() 是
是![]() 的一次函数,求
的一次函数,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求销售利润![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(3)求当![]() 为何值时,
为何值时,![]() 的值最大?最大是多少?
的值最大?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
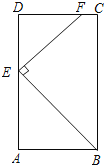
【题目】如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com