
分析 (1)根据实数的混合运算顺序和法则计算可得;
(2)公式法求解可得.
解答 解:(1)原式=1-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$+$\frac{\sqrt{2}}{2}$
=1-1+$\frac{\sqrt{2}}{2}$
=$\frac{\sqrt{2}}{2}$;
(2)原方程可化为x2+2x-3=0,
∵△=22-4×1×(-3)=16>0,
∴x=$\frac{-2±4}{2}$,
∴x1=1,x2=-3.
点评 本题主要考查特殊角的三角函数值、实数的混合运算和解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法和熟记特殊角的三角函数值及实数的混合运算顺序和法则是解题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
| 时间t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
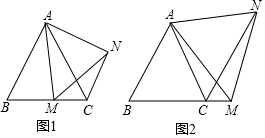
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | … | -0.0001 | 0 | 0.0001 | 1 | 1000 | … |
| $\root{3}{a}$ | … | -0.1 | 0 | 1 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.
如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
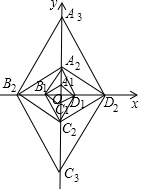 已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1、B1D1相交于点O,以点O为坐标原点,分别以OB1,OA1所在直线为x轴、y轴建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在y轴的正半轴上得到点A1,A2,A3,…,An,则点A2017的坐标为(0,32016).
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1、B1D1相交于点O,以点O为坐标原点,分别以OB1,OA1所在直线为x轴、y轴建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在y轴的正半轴上得到点A1,A2,A3,…,An,则点A2017的坐标为(0,32016).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com