
| 时间t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
分析 (1)设y=kt+b,利用待定系数法即可解决问题.
(2)日利润=日销售量×每公斤利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
(3)列式表示前24天中每天扣除捐赠后的日销售利润,根据函数性质求n的取值范围.
解答 解:(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
$\left\{\begin{array}{l}{k+b=118}\\{3k+b=114}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=120}\end{array}\right.$,
∴y=-2t+120.
将t=30代入上式,得:y=-2×30+120=60.
所以在第30天的日销售量是60kg.
(2)设第x天的销售利润为w元.
当1≤t≤24时,由题意w=(-2t+120)($\frac{1}{4}$t+30-20)=-$\frac{1}{2}$(t-10)2+1250,
∴t=10时 w最大值为1250元.
当25≤t≤48时,w=(-2t+120)(-$\frac{1}{2}$t+48-20)=t2-116t+3360,
∵对称轴t=58,a=1>0,
∴在对称轴左侧w随x增大而减小,
∴t=25时,w最大值=1085,
综上所述第10天利润最大,最大利润为1250元.
(3)设每天扣除捐赠后的日销售利润为m元.
由题意m=(-2t+120)($\frac{1}{4}$t+30-20)-(-2t+120)n=-$\frac{1}{2}$t2+(10+2n)t+1200-120n,
∵在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴-$\frac{10+2n}{2×(-\frac{1}{2})}$>23.5,
∴n>6.75.
又∵n<9,
∴n的取值范围为6.75<n<9.
点评 此题主要考查了二次函数的应用,熟练掌握各函数的性质和图象特征,针对所给条件作出初步判断后需验证其正确性,最值问题需由函数的性质求解时,正确表达关系式是关键.


科目:初中数学 来源: 题型:解答题
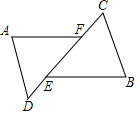 如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.
如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 听 | 说 | 读 | 写 | |
| 张敏得分 | 90 | 80 | 83 | 82 |
| A. | 82 | B. | 83 | C. | 84 | D. | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
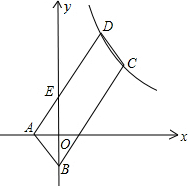 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
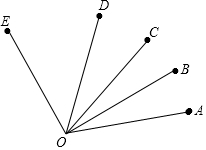 已知:如图,线段OA、OB、OC、OD、OE在同一平面内,且∠AOE=110°,∠AOB=20°.
已知:如图,线段OA、OB、OC、OD、OE在同一平面内,且∠AOE=110°,∠AOB=20°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com