
【题目】我们定义:如果圆的两条弦互相垂直,那么这两条弦互为“十字弦”,也把其中的一条弦叫做另一条弦的“十字弦”.如:如图,已知![]() 的两条弦
的两条弦![]() ,则
,则![]() 、
、![]() 互为“十字弦”,
互为“十字弦”,![]() 是
是![]() 的“十字弦”,
的“十字弦”,![]() 也是
也是![]() 的“十字弦”.
的“十字弦”.
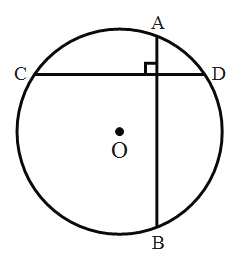
(1)若![]() 的半径为5,一条弦
的半径为5,一条弦![]() ,则弦
,则弦![]() 的“十字弦”
的“十字弦”![]() 的最大值为______,最小值为______.
的最大值为______,最小值为______.
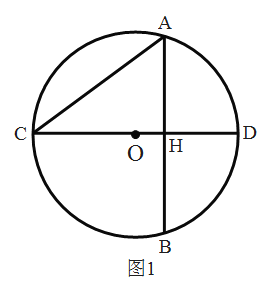
(2)如图1,若![]() 的弦
的弦![]() 恰好是
恰好是![]() 的直径,弦
的直径,弦![]() 与
与![]() 相交于
相交于![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() 、
、![]() 互为“十字弦”;
互为“十字弦”;
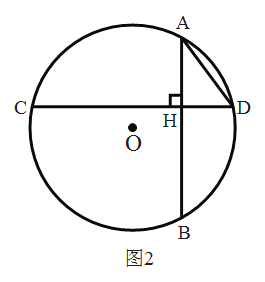
(3)如图2,若![]() 的半径为5,一条弦
的半径为5,一条弦![]() ,弦
,弦![]() 是
是![]() 的“十字弦”,连接
的“十字弦”,连接![]() ,若
,若![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)10,6;(2)见解析;(3)![]() .
.
【解析】
(1)根据“十字弦”定义可得弦![]() 的“十字弦”
的“十字弦”![]() 为直径时最大,当CD过A点或B点时最小;
为直径时最大,当CD过A点或B点时最小;
(2)根据线段长度得出对应边成比例且有夹角相等,证明△ACH∽△DCA,由其性质得出对应角相等,结合90°的圆周角证出AH⊥CD,根据“十字弦”定义可得;
(3)过O作OE⊥AB于点E,作OF⊥CD于点F,利用垂径定理得出OE=3,由正切函数得出AH=![]() DH,设DH=x,在Rt△ODF中,利用线段和差将边长用x表示,根据勾股定理列方程求解.
DH,设DH=x,在Rt△ODF中,利用线段和差将边长用x表示,根据勾股定理列方程求解.
解:(1)当CD为直径时,CD最大,此时CD=10,
∴弦![]() 的“十字弦”
的“十字弦”![]() 的最大值为10;
的最大值为10;
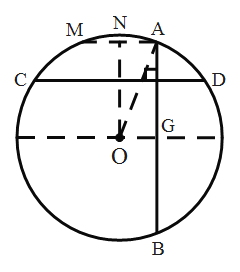
当CD过A点时,CD长最小,即AM的长度,过O点作ON⊥AM,垂足为N,作OG⊥AB,垂足为G,则四边形AGON为矩形,
∴AN=OG,
∵OG⊥AB,AB=8,
∴AG=4,
∵OA=5,
∴由勾股定理得OG=3,
∴AN=3,
∵ON⊥AM,
∴AM=6,
即弦![]() 的“十字弦”
的“十字弦”![]() 的最小值是6.
的最小值是6.
(2)证明:如图,连接AD,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵∠C=∠C,
∴△ACH∽△DCA,
∴∠CAH=∠D,
∵CD是直径,
∴∠CAD=90°,
∴∠C+∠D=90°,
∴∠C+∠CAH=90°,
∴∠AHC=90°,
∴AH⊥CD,
∴![]() 、
、![]() 互为“十字弦”.
互为“十字弦”.
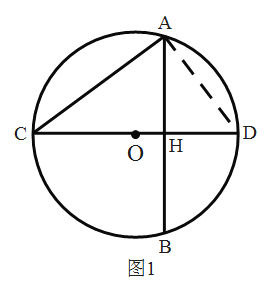
(3)如图,过O作OE⊥AB于点E,作OF⊥CD于点F,连接OA,OD,则四边形OEHF是矩形,∴OE=FH,OF=EH,
∴AE=4,
∴由勾股定理得OE=3,
∴FH=3,
∵tan∠ADH=![]() ,
,
∴tan60°=![]() ,
,
设DH=,则AH=![]() x,
x,
∴FD=3+x,OF=HE=4 -![]() x,
x,
在Rt△ODF中,由勾股定理得,OD2=OF2+FD2,
∴(3+x)2+(4 -![]() x)2=52,
x)2=52,
解得,x=![]() ,
,
∴FD=![]() ,
,
∵OF⊥CD,
∴CD=2DF=![]()
即CD=![]()



 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
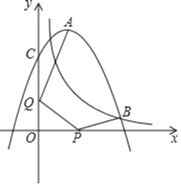
【题目】如图,抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
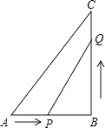
【题目】已知,如图在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发沿AB方向向终点B匀速移动,速度为1cm/s,点Q由点B出发沿BC方向向终点C匀速移动,速度为2cm/s.如果动点P,Q同时从A,B出发,当P或Q到达终点时运动停止.几秒后,以Q,B,P为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
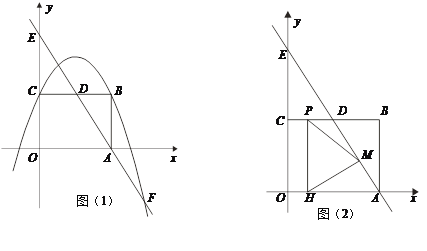
(1)求该抛物线解析式与F点坐标;
(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;
同时,动点M从点A出发,沿线段AE以每秒![]() 个单位长度的速度向终点E运动.过
个单位长度的速度向终点E运动.过
点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,求出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下社团:A.足球、B.机器人、C.航模、D.绘画,学校要求每人只能参加一个社团小丽和小亮准备随机报名一个项目.
(1)求小亮选择“机器人”社团的概率为______;
(2)请用树状图或列表法求两人至少有一人参加“航模”社团的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
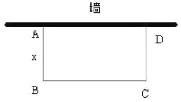
【题目】如图,园林小组的同学用一段长16米的篱笆围成一个一边靠墙的矩形菜园ABCD,墙的长度为9米,设AB的长为x米,BC的长为y米.
(1)①写出y与x的函数关系是: ;
②自变量x的取值范围是 ;
(2)园林小组的同学计划使矩形菜园的面积为30平方米,试求此时边AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
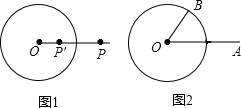
【题目】如图1,⊙O的半径为r,若点P′在射线OP上,满足OP′×OP=r2,则称点P′是点P关于⊙O的“反演点”,如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A'是点A关于⊙O的反演点,求A'B的长为( )
A.![]() B.2
B.2![]() C.2D.4
C.2D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com