
分析 先求得甲、乙独作时的工作效率,然后再求得合作时两人的工作效率,设需要x小时,然后根据合作效率×合作时间=1列方程求解即可.
解答 解:∵甲单独完成要10小时,乙单独完成要15小时,
∴甲独作的工作效率=$\frac{1}{10}$,乙独作的工作效率=$\frac{1}{15}$.
∴合作时,甲的效率=$\frac{1}{10}×\frac{5}{4}$=$\frac{1}{8}$,乙的效率=$\frac{1}{15}×\frac{6}{5}$=$\frac{2}{25}$.
设两人合作完成这项任务需要x小时.
根据题意得:($\frac{1}{8}$+$\frac{2}{25}$)x=1.
解得:x=$\frac{200}{41}$.
故答案为:$\frac{200}{41}$.
点评 本题主要考车的是一元一次方程的应用,求得甲、乙两人合作的工作效率是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
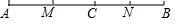 (1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
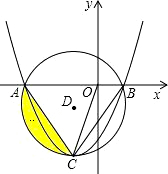 已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.
已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
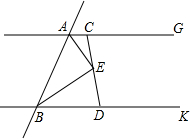 如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.
如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com