
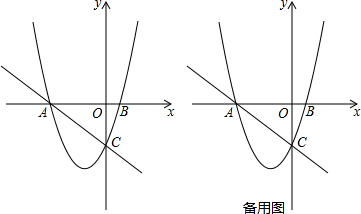
分析 (1)根据自变量与函数值的对应关系,可得A、C点的坐标,可得答案;
(2)①以A为直角顶点时,根据根据等腰三角形的性质,可得∠2的度数,∠3的度数,根据对顶角的性质,可得∠4的度数,根据等腰直角三角形的性质,可得P1H1=H1G,可得关于a的方程,根据解方程,可得a的值,再根据自变量与函数值的对应关系,可得答案;②当C为直角顶点时,根据角的和差,可得∠P2CH2=45°,根据等腰直角三角形的性质,可得关于a的方程,根据解方程,可得a的值,再根据自变量与函数值的对应关系,可得答案;
(3)根据矩形的性质,可得OD与EF的关系,根据垂线段的性质,可得OD的长,根据圆的面积公式.
解答 (1)证明:由抛物线y=x2+2x-3
令y=0,则x2+2x-3=0,解得x1=-3,x2=1,
所以A(-3,0),即OA=3;
令x=0,则y=-3,
所以C(0,-3),即OC=3;
所以OA=OC;
(2)解:①当A为直角顶点时,过点A作AP1⊥AC,交抛物线于点P1,交y轴于点G,过P1作P1H1⊥y轴于点H1,如图1所示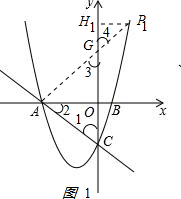 ,
,
由(1)OA=OC,∠AOC=90°
∴△AOC为等腰直角三角形,
∴∠1=∠2=45°.
∵∠P1AC=90°,
∴∠P1AO=45°,∠3=45°,
∴∠4=∠3=45°,
∴∠H1P1G=45°
△AOG,△P1H1G为等腰直角三角形
即OA=OG=3,P1H1=H1G,
设P1(a,a2+2a-3)
则 a=a2+2a-3-3,
解得a1=2,a2=-3(舍)
此时a2+2a-3=5
所以P1坐标是(2,5);
②当C为直角顶点时,过点C作CP2⊥AC,交抛物线于点P2,过P2作P2H2⊥y轴于点H2,如图2所示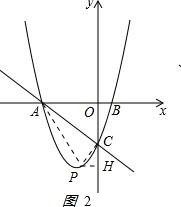 ,
,
∵∠1=45°,∠P2CA=90°,
∴∠P2CH2=45°.
∵∠P2H2C=90°,
∴△P2H2C为等腰直角三角形.
即P2H2=H2C
设P2(a,a2+2a-3)
则-a=-a2-2a+3-3,
解得a1=-1,a2=0(舍去),
此时a2+2a-3=-4
所以P2坐标是(-1,-4)
综上所述,点P坐标是(2,5)或(-1,-4).
(3)△DEF的外接圆面积最小等于$\frac{9π}{8}$.
如图3所示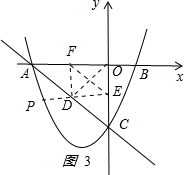 ,
,
因为△DEF为直角三角形,则它外接圆的直径为线段EF,要使圆的面积最小,则直径EF必须取最小值,
又因为EF与OD是矩形OEDF的对角线,所以EF=OD.
因为点到线的距离,垂线段最短,得
OD最小值=$\frac{3}{2}\sqrt{2}$,
故EF=$\frac{3}{2}\sqrt{2}$时,△DEF的外接圆面积最小,得
π($\frac{3\sqrt{2}}{2}$)2=$\frac{9π}{8}$,
△DEF的外接圆面积最小等于$\frac{9π}{8}$.
点评 本题考查了二次函数综合题,利用自变量与函数值的对应关系得出A、C点的坐标是解题关键;利用等腰三角形的性质得出关于a的方程式解题关键,要分类讨论,以防遗漏;利用矩形的性质得出OD与EF的关系是解题关键,又利用了垂线段的性质.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
| 图形 | 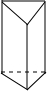 | 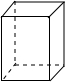 | 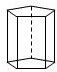 | 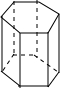 |
| 顶点数a | 6 | 8 | 10 | 12 |
| 棱数b | 9 | 12 | 15 | 18 |
| 面数c | 5 | 6 | 7 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
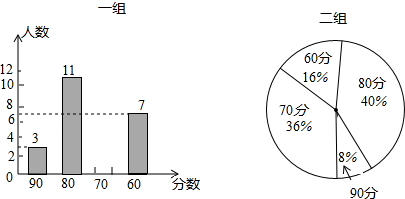
| 平均数 | 中位数 | 众数 | 方差 | |
| 一组 | 74 | 80 | 80 | 104 |
| 二组 | 74 | 70 | 80 | 72 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
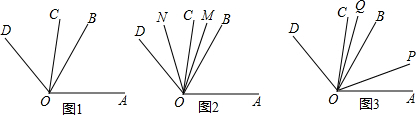
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com