
我们知道,等腰三角形的两个底角相等,即在△ABC中,∵AB=AC,∴∠B=∠C(如图①所示).请根据上述内容探究下面问题:
(1)如图②,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=90°,动点D在BC边上运动,试证明CD=BE且CD⊥BE.
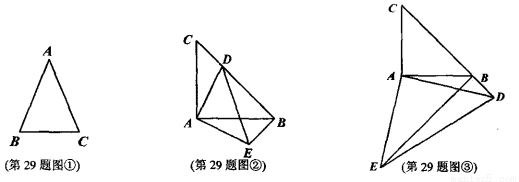
(2)如图③,在(1)的条件下,若动点D在CB的延长线上运动,则CD与BE垂直吗?请在横线上直接写出结论,不必给出证明,答:_______.
(3)如图④,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=90°,动点D在△ABC内运动,试问CD⊥BE还成立吗?若成立,请给出证明过程.

(4)如图④,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=x°(90<x<180),点D在△ABC内,请在横线上直接写出直线CD与直线BE相交所成的锐角(用x的代数式表示).答:直线CD与直线BE相交所成的锐角______________.

(1)详见解析;(2)垂直;(3)不成立;(4)180°-x°
【解析】
试题分析:(1)由证明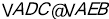 ,可得∠C=∠ABE,即可得证;
,可得∠C=∠ABE,即可得证;
(2)同(1);
(3)同(1)
(4)同上;
试题解析:(1)∵∠CAB=90°,∠DAE=90°,
∴∠CAD=∠BAE,
又∵AC=AB,AD=AE
∴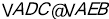
∴∠C=∠ABE,CD=BE
∵∠C+∠B=90°,
∴∠ABE+∠B=90°
∴CD⊥BE
(2)垂直;
(3)不成立,由(1)类似,我们可证得BC⊥BE,故CD不垂直BE;
(4) 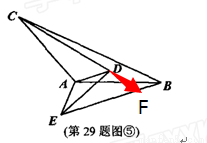
如图,延长CD交BE于F,同(1)我们可证明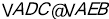 ,得∠ACD=∠ABE,
,得∠ACD=∠ABE,
∴∠CFE=∠CBE+∠BCF
∵AB=AC,∠CAB=∠DAE=x°
∴∠ABC=∠ACB=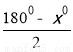
∵∠CBE=∠ABC+∠ABE
∴∠CFE=2∠ABC=180°-x°
考点:全等三角形的判定


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:2016届江西省抚州市黎川县七年级下学期期末数学试卷(解析版) 题型:解答题
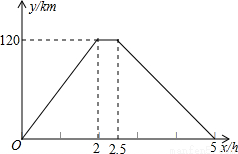
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息回答下列问题:
(1)甲乙两地的距离是 .
(2)到达乙地后卸货用的时间是 .
(3)这辆汽车返回的速度是
查看答案和解析>>
科目:初中数学 来源:2016届江西省吉安市六校七年级下学期联考数学试卷(解析版) 题型:选择题
如图,下列条件中,不能判断直线 ∥
∥ 的是
的是

A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
查看答案和解析>>
科目:初中数学 来源:2016届江苏省苏州市七年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,小明在操场上从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米后,又向左转30°,……,照这样走下去,他第一次回到出发地A点时,一共走了_______米.
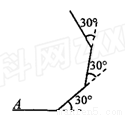
查看答案和解析>>
科目:初中数学 来源:2016届江苏省苏州市相城区七年级下学期期末考试数学试卷(解析版) 题型:解答题
如图1,已知正方形ABCD,把一个直角与正方形叠合,使直角顶点与一重合,当直角的一边与BC相交于E点,另一边与CD的延长线相交于F点时.
(1)证明:BE=DF;
(2)如图2,作∠EAF的平分线交CD于G点,连接EG.证明:BE+DG=EG;
(3)如图3,将图1中的“直角”改为“∠EAF=45°”,当∠EAF的一边与BC的延长线相交于E点,另一边与CD的延长线相交于F点,连接EF.线段BE,DF和EF之间有怎样的数量关系?并加以证明.
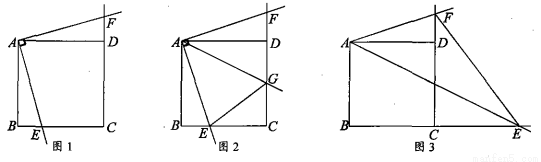
查看答案和解析>>
科目:初中数学 来源:2016届江苏省苏州市吴江区七年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD= °.
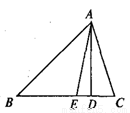
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com