
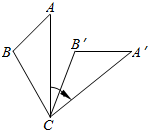
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )| A. | 90° | B. | 80° | C. | 50° | D. | 30° |
分析 首先根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,即可得到∠A′=40°,再有∠B′=110°,利用三角形内角和可得∠A′CB′的度数,进而得到∠ACB的度数,再由条件将△ABC绕着点C顺时针旋转50°后得到△A′B′C′可得∠ACA′=50°,即可得到∠BCA′的度数.
解答 解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°-110°-40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°.
故选:B.
点评 此题主要考查了旋转的性质,关键是熟练掌握旋转前、后的图形全等,进而可得到一些对应角相等.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
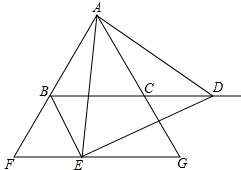 如图:△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
如图:△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4,2 | B. | 2,4 | C. | -4,-2 | D. | -2,-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
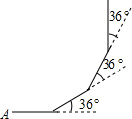 如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了120米.
如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了120米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com