
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm.点P从点B出发,沿BA方向匀速运动,速度为![]() ;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为
;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为![]() .解答下列问题:
.解答下列问题:
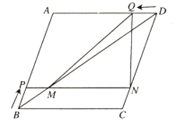
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)是否存在某一时刻![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出
为等腰三角形?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,当
;(3)存在,当![]() 时,
时,![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() ;(4)存在,若
;(4)存在,若![]() 时,
时,![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() 时,
时,![]()
【解析】
(1)连接![]() ,证明
,证明![]() 得到
得到![]() ,根据垂直平分线的性质得出
,根据垂直平分线的性质得出![]() ,求出t的值即可;
,求出t的值即可;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,由菱形的性质求出
,由菱形的性质求出![]() ,证明
,证明![]() ,得
,得![]() ,再求出
,再求出![]() ,根据三角形面积公式即可得出结论;
,根据三角形面积公式即可得出结论;
(3)假设存在某一时刻![]() ,根据
,根据![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() 列方程求解即可;
列方程求解即可;
(4)分![]() ,
,![]() ,
,![]() 三种情况分别求解即可
三种情况分别求解即可
解:(1)连接![]()
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]() ∴
∴![]()
若点![]() 在线段
在线段![]() 的垂直平分线上
的垂直平分线上
∴![]() ∴
∴![]() ∴
∴![]()
∴当![]() 时,点
时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
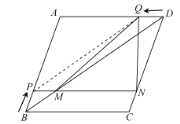
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
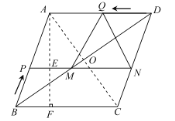
∵![]()
∴![]()
连接![]() ,交
,交![]() 于点
于点![]() ,根据题意
,根据题意![]() ,
,
∴![]()
菱形面积:![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴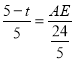
∴![]()
∵![]()
∴![]() 的高等于
的高等于![]()
∵四边形![]() 是菱形
是菱形
∴![]() ,
,
∴![]()
∴![]()
![]()
∴![]() 与
与![]() 的函数关系式是
的函数关系式是![]() .
.
(3)假设存在某一时刻![]() ,使
,使![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() ,
,
则![]()
解得,![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
答:当![]() 时,
时,![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() .
.
(4)若![]() 时,
时,
由(2)得![]()
由题意得,![]() ,
,![]()
∴过Q作![]() 于点G,
于点G,
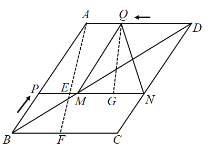
∵![]() ,
,![]()
∴![]()
在![]() 中,
中,![]()
![]()
![]()
∴![]() ;
;
若![]() 时,
时,
过N作![]() 于J,如图,
于J,如图,
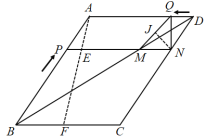
则![]() ,
,
![]()
而![]()
∴![]() ;
;
若![]() 时,
时,![]() ,
,
∴![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
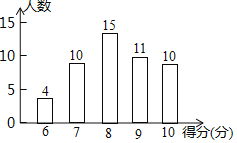
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)
请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三条边相等的四边形称为三等边四边形.
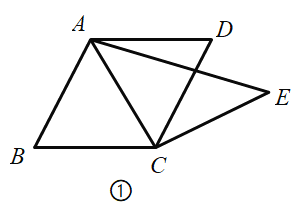
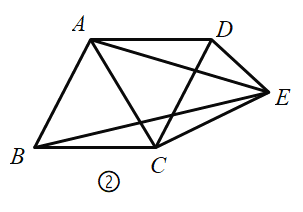
(1)如图①,平行四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() ,将线段
,将线段![]() 绕点
绕点![]() 旋转一个角度
旋转一个角度![]() 至
至![]() ,连接
,连接![]() .
.
①求证:四边形![]() 是三等边四边形;
是三等边四边形;
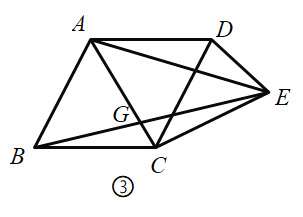
②如图②,连接![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图,在(1)的条件下,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,求以
,求以![]() ,
,![]() 和
和![]() 为边的三角形的面积.
为边的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地捐赠了600吨物资支援武汉抗击新冠肺炎,准备安排A、B两种类型的货车把这批物资从甲地快速送到武汉,若安排A型货车5辆、B型货车6辆,一共需补贴油费3800元;若安排A型货车3辆、B型货车2辆,一共需补贴油费1800元.
(1)从甲地到武汉,A、B两种类型货车每辆各需补贴油费多少元?
(2)A型货车每辆可装15吨物资,B型货车每辆可装12吨物资,若安排的B型货车的数量是A型货车的2倍还多4辆,且A型车最多可安排18辆.运送这批物资共有哪些安排,其中补贴的总油费最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,且
上一点,且![]() ,点
,点![]() 在边
在边![]() 上,过点
上,过点![]() 、
、![]() 、
、![]() 作圆
作圆![]() ,交边
,交边![]() 或其延长线于
或其延长线于![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,设
,设![]() (
(![]() ).
).
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求弧
,求弧![]() 的长;
的长;
(4)若圆![]() 经过矩形的两个顶点时,直接写出
经过矩形的两个顶点时,直接写出![]() 的值.
的值.
(注:![]() ,
,![]() ,
,![]() )
)
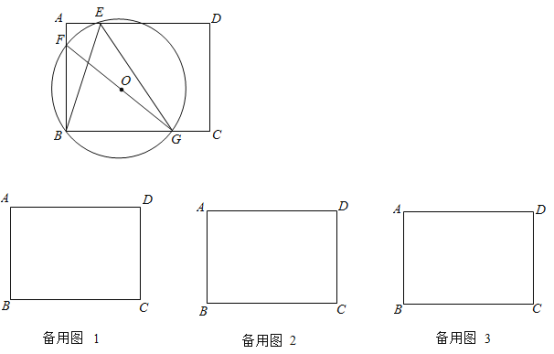
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
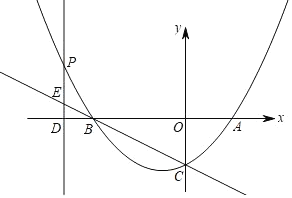
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B(5,0),与y轴交于点C,抛物线的顶点为M(2,-9),连接BM,点P为线段BM上的一个动点.
(1)求二次函数的解析式.
(2)过点P作x轴的垂线,垂足为点Q,求四边形ACPQ面积的最大值.
(3)是否存在点P,使得以P、M、C为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com