
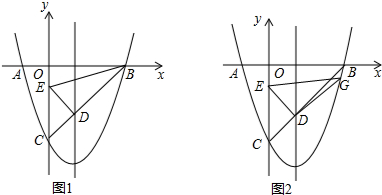
���� ��1���ȸ�����������x��Ľ����������A��-1��0����B��3��0�������öԳ��Կɵ������ߵĶԳ���Ϊֱ��x=1�������C��0��-3����Ȼ�����ô���ϵ������ֱ��BC�Ľ���ʽ����x=1ʱ��y=-x+3=-3����D������Ϊ��1��-2����
��2����ͼ1�����жϡ�OBCΪ����ֱ�������Σ����OCB=��OBC=45�㣬�ټ����CD=$\sqrt{2}$��Ȼ��ͨ�������BDEΪֱ��������ʱm��ֵ��ȷ����BDEΪ�۽�������ʱ��m��ȡֵ��Χ��
��3���������ۣ��ٵ���G�ڶԳ����Ҳ����������ʱ����ͼ2����DF��y����F��GH��DF��H����G��t��t2-2t-3������GH=t2-2t-3-��-2��=t2-2t-1������ת�����ʵá�EDG=90�㣬����֤��Rt��EDF��Rt��DGH���������Ƶ����ʵ�$\frac{DF}{GH}$=$\frac{DE}{DG}$����$\frac{DE}{DG}$=2����$\frac{1}{GH}$=2����t2-2t-1=$\frac{1}{2}$�����t1=1-$\frac{\sqrt{10}}{2}$����ȥ����t2=1+$\frac{\sqrt{10}}{2}$����ʱG������Ϊ��1+$\frac{\sqrt{10}}{2}$��-$\frac{3}{2}$������$\frac{DE}{DG}$=$\frac{1}{2}$����$\frac{1}{GH}$=$\frac{1}{2}$����t2-2t-1=2�����t1=-1����ȥ����t2=3����ʱG������Ϊ��3��0�����ڵ���G�ڶԳ���������������ʱ����ͬ���ķ����ɵ�G������Ϊ��1-$\frac{\sqrt{10}}{2}$��-$\frac{3}{2}$����-1��0����
��� �⣺��1����y=0ʱ��x2-2x-3=0�����x1=-1��x2=3����A��-1��0����B��3��0��
���������ߵĶԳ���Ϊֱ��x=1��
��x=0ʱ��y=x2-2x-3=-3����C��0��-3����
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��3��0����C��0��-3�������$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$��
����ֱ��BC�Ľ���ʽΪy=x-3��
��x=1ʱ��y=-x+3=-3����D������Ϊ��1��-2����
��2����ͼ1����B��3��0����C��0��-3��
���OBCΪ����ֱ�������Σ�
���OCB=��OBC=45�㣬
��D��1��-2����
��CD=$\sqrt{{1}^{2}+��-2+3��^{2}}$=$\sqrt{2}$��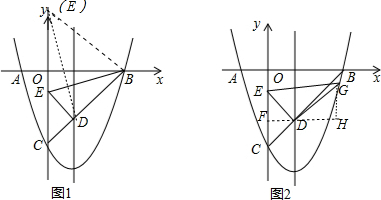
����EDB=90��ʱ�����CDEΪ����ֱ�������Σ�
��CE=$\sqrt{2}$CD=$\sqrt{2}$��$\sqrt{2}$=2��
��OE=3-2=1����ʱE��0��-1����
�൱m��-1��m��-3ʱ����EDBΪ�۽ǣ���EDBΪ�۽������Σ�
����EBD=90��ʱ�����OBEΪ����ֱ�������Σ�
��OE=OB=3����ʱE��0��3����
�൱m��3ʱ����EDBΪ�۽ǣ���EDBΪ�۽������Σ�
��m��ȡֵ��ΧΪm��3��m��-1��m��-3��
��3�����ڣ�
�ٵ���G�ڶԳ����Ҳ����������ʱ����ͼ2����DF��y����F��GH��DF��H��
��G��t��t2-2t-3������GH=t2-2t-3-��-2��=t2-2t-1��
������DE�Ƶ�D˳ʱ�뷽����ת90�㣬�������߽���ΪG��
���EDG=90�㣬
���EDF+��GDH=90�㣬
����EDF+��DEF=90�㣬
���DEF=��GDH��
��Rt��EDF��Rt��DGH��
��$\frac{DF}{GH}$=$\frac{DE}{DG}$��
��$\frac{DE}{DG}$=2����$\frac{1}{GH}$=2����t2-2t-1=$\frac{1}{2}$�����t1=1-$\frac{\sqrt{10}}{2}$����ȥ����t2=1+$\frac{\sqrt{10}}{2}$����ʱG������Ϊ��1+$\frac{\sqrt{10}}{2}$��-$\frac{3}{2}$����
��$\frac{DE}{DG}$=$\frac{1}{2}$����$\frac{1}{GH}$=$\frac{1}{2}$����t2-2t-1=2�����t1=-1����ȥ����t2=3����ʱG������Ϊ��3��0����
�ڵ���G�ڶԳ���������������ʱ����ͬ���ķ����ɵ�G������Ϊ��1-$\frac{\sqrt{10}}{2}$��-$\frac{3}{2}$����-1��0����
����������G��������1+$\frac{\sqrt{10}}{2}$��-$\frac{3}{2}$����3��0����1-$\frac{\sqrt{10}}{2}$��-$\frac{3}{2}$����-1��0����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ͵���ֱ�������ε����ʣ������ô���ϵ������ֱ�߽���ʽ�����������Ʊȼ����߶εij����ѵ�����ι������������κͷ�������˼������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
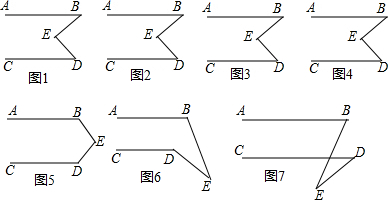
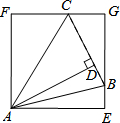 ��ͼ����ABC�У���BAC=45�㣬AD��BC��BD=1��CD=3������ABD��AB�۵��õ���ABE������ACD��AC�۵��õ���ACF���ӳ�EB��FC���ڵ�G��
��ͼ����ABC�У���BAC=45�㣬AD��BC��BD=1��CD=3������ABD��AB�۵��õ���ABE������ACD��AC�۵��õ���ACF���ӳ�EB��FC���ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
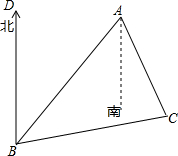 ��ͼ��ʾ��B����A������ƫ��45�㷽���ϣ�C����A������ƫ��30�㷽��C����B���ı�ƫ��85�㣬���ACB�Ƕ��ٶȣ�����ʾ����������ABC�У���BAC+��ABC+��ACB=180�㣩
��ͼ��ʾ��B����A������ƫ��45�㷽���ϣ�C����A������ƫ��30�㷽��C����B���ı�ƫ��85�㣬���ACB�Ƕ��ٶȣ�����ʾ����������ABC�У���BAC+��ABC+��ACB=180�㣩�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����E��������ABCD��һ�㣬����AE��BE��DE����AE=2��BE=$\sqrt{15}$����AED=135�㣬��������ABCD�����Ϊ11+2$\sqrt{14}$��
��ͼ����E��������ABCD��һ�㣬����AE��BE��DE����AE=2��BE=$\sqrt{15}$����AED=135�㣬��������ABCD�����Ϊ11+2$\sqrt{14}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
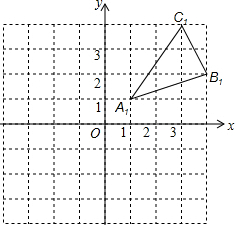 ��ͼ����A1B1C1�ǡ�ABC����ƽ��4����λ���Ⱥ�õ��ģ����������������ֱ�ΪA1��1��1����B1��4��2����C1��3��4����
��ͼ����A1B1C1�ǡ�ABC����ƽ��4����λ���Ⱥ�õ��ģ����������������ֱ�ΪA1��1��1����B1��4��2����C1��3��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �װ� | B�� | ������һ������ | C�� | �Ұ� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
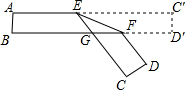 ��һ������Ա߷ֱ�ƽ�е�ֽ���۵�����ͼ��ʾ��EF���ۺۣ�����EFB=34�㣬���BFD����Ϊ112�㣮
��һ������Ա߷ֱ�ƽ�е�ֽ���۵�����ͼ��ʾ��EF���ۺۣ�����EFB=34�㣬���BFD����Ϊ112�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com