
【题目】在平面直角坐标系中,点A(1,0),已知抛物线y=﹣x2+mx﹣2m(m是常数),顶点为P.
(1)当抛物线经过点A时,求顶点P坐标;
(2)等腰Rt△AOB,点B在第四象限,且OA=OB.当抛物线与线段OB有且仅有两个公共点时,求m满足的条件;
(3)无论m取何值,该抛物线都经过定点H.当∠AHP=45°,求此抛物线解析式.

【答案】(1)顶点P坐标(﹣![]() ,
,![]() );(2)m>2
);(2)m>2![]() ﹣3;(3)y=﹣x2+
﹣3;(3)y=﹣x2+![]() x﹣
x﹣![]() 或y=﹣x2+
或y=﹣x2+![]() x﹣
x﹣![]()
【解析】
(1)将点A坐标代入解析式,可求m的值,即可求解;
(2)先求出点B坐标,由抛物线与线段OB有且仅有两个公共点,可列不等式,可求解;
(3)当x=2时,y=﹣4+2m﹣2m=﹣4,则抛物线都经过定点H(2,﹣4),分点P在AH的左侧或右侧两种情况讨论,构造全等三角形,求出BH解析式,即可求解.
解:(1)∵抛物线经过点A,
∴0=﹣1+m﹣2m,
∴m=﹣1,
∴抛物线解析式为:y=﹣x2﹣x+2=﹣(x+![]() )2+
)2+![]() ,
,
∴顶点P坐标(﹣![]() ,
,![]() );
);
(2)∵点A(1,0),OA=OB,
∴点B(1,﹣1)
设直线OB的解析式为![]()
将点B代入得![]()
∴直线OB解析式为:y=﹣x,
∵抛物线与线段OB有且仅有两个公共点,
∴﹣x=﹣x2+mx﹣2m,
∴△=(m+1)2﹣8m>0,
∴m>2![]() ﹣3,或m<﹣2
﹣3,或m<﹣2![]() ﹣3,
﹣3,
∵抛物线与线段OB有且仅有两个公共点,
∴![]()
∴m≥0,
∴m>2![]() ﹣3,
﹣3,
(3)∵当x=2时,y=﹣4+2m﹣2m=﹣4,
∴抛物线都经过定点H(2,﹣4),
若点P在AH的左侧,如图1,过点A作AB⊥PH,过点B作BD⊥OA,过点H作HC⊥BD于C,
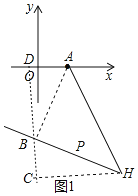
∵∠AHP=45°,AB⊥PH,
∴∠BAH=∠AHB=45°,
∴AB=BH,
∵∠DBA+∠CBH=90°,∠DBA+∠DAB=90°,
∴∠DAB=∠CBH,且AB=BH,∠ADB=∠BCH=90°,
∴△DAB≌△CBH(AAS)
∴AD=BC,BD=CH,
∵BC+BD=4,CH﹣AD=1,
∴BD=CH=![]() ,BC=AD=
,BC=AD=![]() ,
,
∴点B(﹣![]() ,﹣
,﹣![]() )
)
设直线BH解析式为:y=kx+b,
∴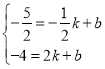
解得: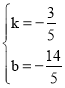
∴直线BH解析式为:y=﹣![]() x﹣
x﹣![]() ,
,
∵y=﹣x2+mx﹣2m![]()
∴P(![]() ,
,![]() )
)
∵点P(![]() ,
,![]() )在直线BH上,
)在直线BH上,
∴![]() =﹣
=﹣![]() ×
×![]() ﹣
﹣![]()
∴m1=4,m2=![]() ,
,
∵当m=4时,点P(2,﹣4)与点H重合,
∴m=![]()
∴抛物线解析式:y=﹣x2+![]() x﹣
x﹣![]() ,
,
若点P在AH的右侧,如图2,
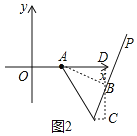
同理可求:直线BH解析式为:y=![]() x﹣
x﹣![]() ,
,
∵点P(![]() ,
,![]() )在直线BH上,
)在直线BH上,
∴![]() =
=![]() ×
×![]() ﹣
﹣![]() ,
,
∴m1=4,m2=![]() ,
,
∴抛物线解析式:y=﹣x2+![]() x﹣
x﹣![]() ,
,
综上所述,抛物线解析式为y=﹣x2+![]() x﹣
x﹣![]() 或y=﹣x2+
或y=﹣x2+![]() x﹣
x﹣![]() .
.


科目:初中数学 来源: 题型:
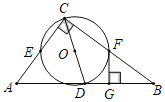
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,连接CD,点O是CD的中点,到点O的距离等于OC的所有点组成图形M,图形M分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与图形M的位置关系,并说明理由;
(2)若AC=3,∠B=30°,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用家用燃气灶烧开同一壶水所需的燃气量![]() (单位:
(单位:![]() )与旋钮的旋转角度
)与旋钮的旋转角度![]() (单位:度)(
(单位:度)(![]() )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度
)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度![]() 与燃气量
与燃气量![]() 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
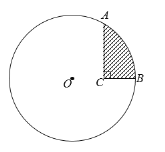
【题目】如图,⊙O的半径为![]() ,A、B为⊙O上两点,C为⊙O内一点,AC⊥BC,AC=
,A、B为⊙O上两点,C为⊙O内一点,AC⊥BC,AC=![]() ,BC=
,BC=![]() .
.
(1)判断点O、C、B的位置关系;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
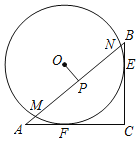
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.直径为5的⊙O分别与AC、BC相切于点F、E,与AB交于点M、N,过点O作OP⊥MN于P,则OP的长为( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
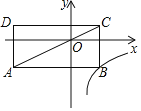
【题目】如图,在直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数y=![]() (k≠0,x>0)的图像上,点D的坐标为(-4,1),则K的值为( )
(k≠0,x>0)的图像上,点D的坐标为(-4,1),则K的值为( )
A.![]() B.
B.![]() C.4D.-4
C.4D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
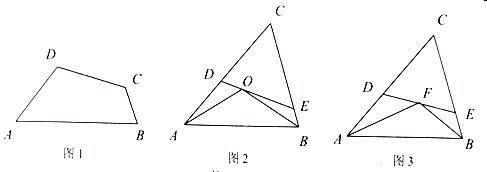
【题目】定义:有两个相邻内角和等于另两个内角和的一半的四边形称为半四边形,这两个角的夹边称为对半线.
(1)如图1,在对半四边形![]() 中,
中,![]() ,求
,求![]() 与
与![]() 的度数之和;
的度数之和;
(2)如图2,![]() 为锐角
为锐角![]() 的外心,过点
的外心,过点![]() 的直线交
的直线交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是对半四边形;
是对半四边形;
(3)如图3,在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,当
,当![]() 为对半四边形
为对半四边形![]() 的对半线时,求
的对半线时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
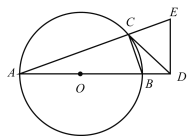
【题目】如图,已知点![]() 在
在![]() 的直径
的直径![]() 延长线上,点
延长线上,点![]() 为
为![]() 上,过
上,过![]() 作
作![]() ,与
,与![]() 的延长线相交于
的延长线相交于![]() ,
,![]() 为
为![]() 的切线,
的切线,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的长;
的长;
(3)若![]() 的平分线与
的平分线与![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的内心,求
的内心,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com