
 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).分析 (1)由于a>0,则计算判别式的值得到△>0,于是根据判别式的意义可判断方程有两个不相等的实数根;
(2)利用求根公式可得到x1=1,x2=1-$\frac{2}{a}$,于是得到y=ax2+x1=a-1;
(3)把y≤-3a2+1理解为一次函数y=a-1与二次函数y=-3a2+1比较函数值的大小,先求出两函数的交点坐标,然后写出抛物线都在直线上方所对应的自变量的范围即可,注意a>0.
解答 (1)证明:∵△=[-2(a-1)]2-4a(a-2)=4.
∴△>0,
∴方程有两个不相等的实数根;
(2)解:x=$\frac{2(a-1)±2}{2a}$=$\frac{a-1±1}{a}$
∵a>0,x1>x2,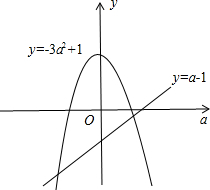
∴x1=1,x2=1-$\frac{2}{a}$,
∴y=ax2+x1=a-1,
即这个函数的表达式为y=a-1(a>0);
(3)解:如图,
解方程组$\left\{\begin{array}{l}{y=a-1}\\{y=-3{a}^{2}+1}\end{array}\right.$得$\left\{\begin{array}{l}{a=-1}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{y=-\frac{1}{3}}\end{array}\right.$,
即抛物线y=-3a2+1与直线y=a-1的两个交点坐标为(-1,-2)、($\frac{2}{3}$,-$\frac{1}{3}$),
当y≤-3a2+1时,0<a≤$\frac{2}{3}$.
故答案为0<a≤$\frac{2}{3}$.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系:△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $3\sqrt{2}-2\sqrt{2}=1$ | C. | $\sqrt{3^2}=3$ | D. | $\sqrt{9}=±3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
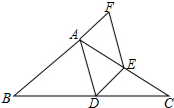 如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=$\frac{1}{2}$AB,连接EF,判断四边形ADEF的形状,并加以证明.
如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=$\frac{1}{2}$AB,连接EF,判断四边形ADEF的形状,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
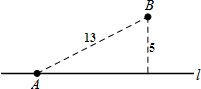 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
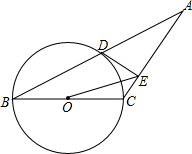 如图,在△ABC中,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
如图,在△ABC中,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
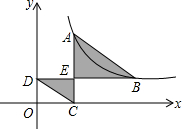 如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )
如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )| A. | 5 | B. | 6 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com