
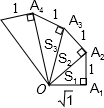
 观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数).
观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数). 分析 这是一个规律性题目,第一个三角形的斜边正好是第二个三角形的直角边,依次进行下去,且有一个直角边的边长为1.从而可求出面积.
解答 解:根据勾股定理:
第一个三角形中:OA12=1+1,S1=1×1÷2;
第二个三角形中:OA22=OA12+1=1+1+1,S2=OA1×1÷2=$\sqrt{2}$×1÷2;
第三个三角形中:OA32=OA22+1=1+1+1+1,S3=OA2×1÷2=$\sqrt{3}$×1÷2;
…
第n个三角形中:Sn=$\sqrt{n}$×1÷2=$\frac{\sqrt{n}}{2}$.
故答案为:$\frac{\sqrt{n}}{2}$.
点评 本题主要考查了勾股定理的应用,根据勾股定理,逐一进行计算,从中寻求规律,进行解答是解题的关键.


科目:初中数学 来源: 题型:选择题
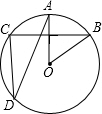 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{3}{2}$ | B. | x<$\frac{3}{2}$ | C. | x>3 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
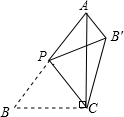 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是1.
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
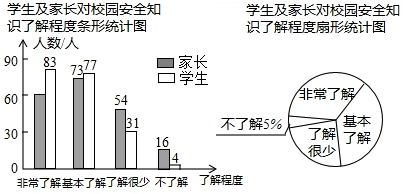
| A. | 1330 | B. | 1350 | C. | 1682 | D. | 1850 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
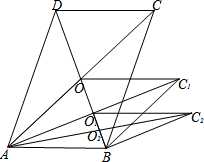 如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.
如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.| A. | ${(\frac{1}{2})^{n-1}}$a | B. | ${(\frac{1}{2})^n}$a | C. | ${(\frac{1}{2})^{n+1}}$a | D. | ${(\frac{1}{3})^n}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com