

分析 (1)过点C作CH⊥OA于H,由勾股定理求出OC,得出CB,即可得出结果;
(2)分两种情况:①当0≤t≤5时,由菱形的性质得出OA=AB=BC=OC=5,OC∥AB.由平行线得出△OMN∽△OAC,得出比例式求出OM即可;
②当5≤t≤10时,设直线MN与OA交于点E.,同①可得AM=$\frac{5}{2}$.在证出△AEM∽△OAC.得出对应边成比例求出AM=AE,得出OE即可;
(3)分两种情况①当0≤t<5时,求出△OAC的面积,再由相似三角形的性质得出$\frac{{{S_{△OMN}}}}{{{S_{△OAC}}}}={({\frac{OM}{OA}})^2}$,即可得出结果;
②当5≤t≤10时,过点M作MT⊥x轴于T,由△BMN∽△AME可知,MT=$\frac{4}{5}$(t-5),得出S△OMN=S△ONE-S△OME=$-\frac{2}{5}{({t-5})^2}+10$;即可得出结果.
解答 解:(1)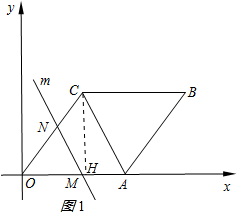 过点C作CH⊥OA于H,如图1所示:
过点C作CH⊥OA于H,如图1所示:
∵C (3,4),
∴CH=4,OH=3,
∴OC=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵四边形OABC是菱形,
∴CB=OC=5,5+3=8,
∴点B的坐标为(8,4);
(2)分两种情况:
①当0≤t≤5时,
如图2所示: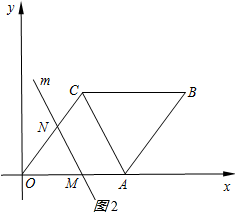
∵四边形OABC是菱形,
∴OA=AB=BC=OC=5,OC∥AB.
∵MN∥AC,
∴△OMN∽△OAC,
∴$\frac{MN}{AC}=\frac{OM}{OA}$.
∵$MN=\frac{1}{2}AC$,
∴$OM=\frac{1}{2}OA$
∴$OM=\frac{5}{2}$,
∴$t=\frac{5}{2}$.
②当5≤t≤10时,如图3所示: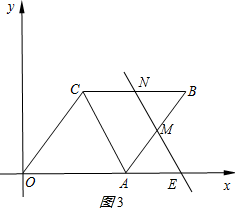
设直线MN与OA交于点E.,同①可得AM=$\frac{5}{2}$.
∵OC∥AB,MN∥AC,
∴∠COA=∠MAE,∠CAO=∠MEA,
∴△AEM∽△OAC.
∴$\frac{AE}{OA}=\frac{AM}{OC}$.
∵OC=OA,
∴AM=AE,
∴$OE=\frac{15}{2}$,
∴$t=\frac{15}{2}$.
综上所述:$t=\frac{5}{2}$或$t=\frac{15}{2}$.
(3)分两种情况: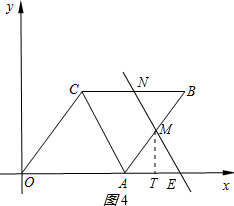
①当0≤t<5时(如图1),${S_{△OAC}}=\frac{1}{2}OA•CH=10$.
∵△OMN∽△OAC,
∴$\frac{{{S_{△OMN}}}}{{{S_{△OAC}}}}={({\frac{OM}{OA}})^2}$,即$\frac{{S}_{△OMN}}{10}=(\frac{t}{5})^{2}$,
∴$S=\frac{2}{5}{t^2}$(0≤t<5);
②当5≤t≤10时,过点M作MT⊥x轴于T,如图4所示:
由△BMN∽△AME可知,MT=$\frac{4}{5}$(t-5),
∴S△OMN=S△ONE-S△OME=$-\frac{2}{5}{({t-5})^2}+10$;
综上所述:S=$\left\{\begin{array}{l}{\frac{2}{5}{t}^{2}(0≤t<5)}\\{-\frac{2}{5}(t-5)^{2}+10(5≤t≤10)}\end{array}\right.$;
∴当t=5时,S最大值=10.
点评 本题考查了菱形的性质、勾股定理、相似三角形的判定与性质、平行线的性质、坐标与图形性质、二次函数的最值问题等知识;本题综合性强,有一定难度,特别是(2)和(3)中,需要进行分类讨论才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
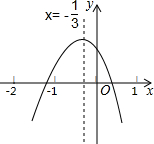 小明从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察到下面四条信息:①ab>0;②a+b+c<0;③b+2c>0;④a=$\frac{3}{2}$b.你认为其中正确信息的个数有( )
小明从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察到下面四条信息:①ab>0;②a+b+c<0;③b+2c>0;④a=$\frac{3}{2}$b.你认为其中正确信息的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测试项目 | 测试成绩/分 | |
| A | B | |
| 创新 | 85 | 70 |
| 综合知识 | 50 | 80 |
| 语言 | 88 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知P、M、N三点,按下面要求画出图形;
如图,已知P、M、N三点,按下面要求画出图形;查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com