练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
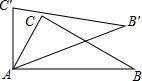
    4．如图所示，在△ABC中，∠CAB=70°，将△ABC绕点A旋转到△A′B′C′的位置，使得C′A⊥AB，则∠BAB′=（　　）
    A．10°B．20°C．30°D．50°

    分析 根据旋转的性质得到∠B′AC′=∠CAB=70°，又知道C′A⊥AB，所以有∠C′AB=∠B′AC′+∠BAB′=90°，最后可以算出∠BAB′的度数．

    解答 解：∵△ABC绕点A旋转到△A′B′C′的位置，
    ∴∠B′AC′=∠CAB，
    ∵∠CAB=70°，
    ∴∠B′AC′=∠CAB=70°，
    又∵C′A⊥AB，
    ∴∠C′AB=∠B′AC′+∠BAB′=90°，
    ∴∠BAB′=90°-70°=20°，
    故选：B．

    点评 本题主要考查了旋转的性质的知识，解答本题的关键是求出∠CAC′=∠BAB′，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．某服装店用10000元购进A，B两种新式服装，按标价售出后可获得毛利润5400元（毛利润=售价-进价），这两种服装的进价、标价如表所示：

    （1）这两种服装各购进的件数；
    （2）如果A种服装按标价的8折出售，要使这批服装全部售出后毛利润不低于2000元，则B种服装至多按标价的几折出售？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．函数y=$\frac{\sqrt{x}}{x+2}$的自变量x的取值范围是x≥0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

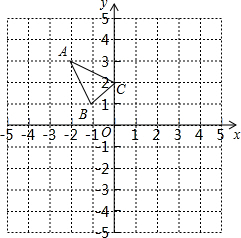    12．△ABC在平面直角坐标系xOy中的位置如所示．
    （1）作△ABC关于点C成中心对称的△A1B1C1；
    （2）将△A1B1C1向右平移3个单位，作出平移后的△A2B2C2；
    （3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标；
    （4）在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

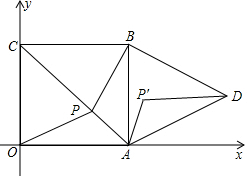    19．如图，正方形ABCO的边长为1，顶点A、C分别在x、y轴上，以AB为边向右作等边三角形ADB，点P为对角线AC上的动点．
    （1）点B的坐标为（1，1），点D的坐标为（1+$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）；当点P的坐标为（$\frac{1}{2}$，$\frac{1}{2}$）时，PO+PB的值最小（坐标可保留根号）；
    （2）将AP绕点A顺时针旋转60度至AP′位置
    ①证明：BP=DP′；
    ②在线段AC上是否存在点P，使得BP+OP+AP的值最小？若不存在请说明理由；若存在，请简要说明理由并求出这个最小值（结果精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

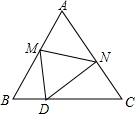    9．如图，在等边三角形纸片△ABC中，将纸片折叠，点A落在BC边上的点D处，MN为折痕，当DN⊥NC时，CN=1，则A、D两点之间的距离为$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

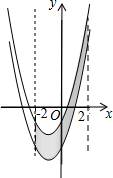    16．如图，已知抛物线y=x2+2x-3，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线与经过点（-2，0），（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m，则下列图象中，能表示s与m的函数关系的图象大致是（　　）
    A．B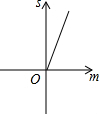．C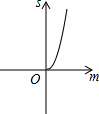．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知点P是函数y=$\sqrt{3}$|x+1|图象上的点，点O（0，0），A（1，$\sqrt{3}$），求△OAP的面积S与x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

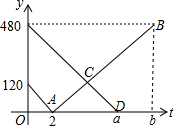    14．甲乙两城市之间有一条公路相连，公路中途穿过丙市，现有两位司机M、N相约各自同时从甲乙两地出发，途中M将一件物品交给N，已知M从甲市到丙市，N从乙市到甲市，N的速度是M的$\frac{3}{4}$，他们开车距离丙市的距离y（千米）与行驶的时间t（小时）的函数图象如图所示．
    （1）求a的值；
    （2）求AB所在直线的函数解析式及C点的坐标；
    （3）何时他们相距300千米？

    查看答案和解析>>

    同步练习册答案