
分析 分两种情况①当x>-1时,y=$\sqrt{3}$x+$\sqrt{3}$,设P(x,$\sqrt{3}$x+$\sqrt{3}$),作AM⊥y轴于M,PN⊥y轴于N,根据S=S梯形ANMP-S△POM-S△PON即可求得;②当x<-1时,y=-$\sqrt{3}$x-$\sqrt{3}$,设P(x,-$\sqrt{3}$x-$\sqrt{3}$),作AN⊥x轴于N,PM⊥x轴于M,根据S=S梯形ANMP-S△POM-S△PON即可求得.
解答 解:∵点P是函数y=$\sqrt{3}$|x+1|图象上的点,
当x>-1时,y=$\sqrt{3}$x+$\sqrt{3}$,
设P(x,$\sqrt{3}$x+$\sqrt{3}$),如图1,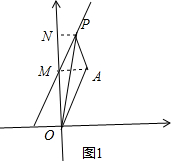
作AM⊥y轴于M,PN⊥y轴于N,
∴S=S梯形AMNP+S△AOM-S△PON
=$\frac{1}{2}$(x+1)($\sqrt{3}$x+$\sqrt{3}$-$\sqrt{3}$)+$\frac{1}{2}$×$1×\sqrt{3}$-$\frac{1}{2}$x($\sqrt{3}$x+$\sqrt{3}$)
=$\frac{\sqrt{3}}{2}$.
当x<-1时,y=-$\sqrt{3}$x-$\sqrt{3}$,
设P(x,-$\sqrt{3}$x-$\sqrt{3}$),如图2,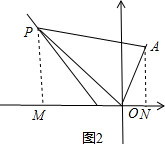
作AN⊥x轴于N,PM⊥x轴于M,
∴S=S梯形ANMP-S△POM-S△PON
=$\frac{1}{2}$(-$\sqrt{3}$x-$\sqrt{3}$+$\sqrt{3}$)(-x+1)-$\frac{1}{2}$×(-x)(-$\sqrt{3}$x-$\sqrt{3}$)-$\frac{1}{2}$×$1×\sqrt{3}$
=-$\sqrt{3}x$-$\frac{\sqrt{3}}{2}$(x<-1).
综上,△OAP的面积S与x的函数关系式为:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}(x>-1)}\\{-\sqrt{3}x-\frac{\sqrt{3}}{2}(x<-1)}\end{array}\right.$.
点评 本题考查了一次函数图象上点的坐标特征,根据题意得出函数y=$\sqrt{3}$|x+1|为y=$\left\{\begin{array}{l}{y=\sqrt{3}x+\sqrt{3}(x>-1)}\\{y=-\sqrt{3}x-\sqrt{3}(x<-1)}\end{array}\right.$,分类讨论的思想是本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
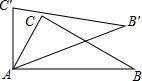 如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )| A. | 10° | B. | 20° | C. | 30° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.
如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
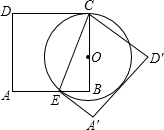 如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.
如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
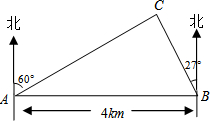 如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).
如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com