
已知抛物线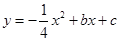 与
与 轴交于
轴交于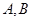 两点,与
两点,与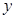 轴交于点
轴交于点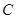 ,连结
,连结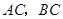 ,
,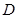 是线段
是线段 上一动点,以
上一动点,以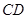 为一边向右侧作正方形
为一边向右侧作正方形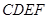 ,连结
,连结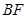 .若
.若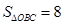 ,
,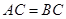 .
.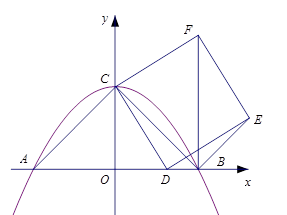
(1)求抛物线的解析式;
(2)求证: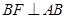 ;
;
(3)求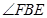 的度数;
的度数;
(4)当 点沿
点沿 轴正方向移动到点
轴正方向移动到点 时,点
时,点 也随着运动,则点
也随着运动,则点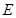 所走过的路线长是 .
所走过的路线长是 .
(1)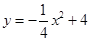 ;(2)由(1)得点B、C的坐标,即可得到
;(2)由(1)得点B、C的坐标,即可得到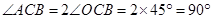 ,证得
,证得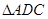 ≌
≌ ,根据全等三角形的性质求解即可;(3)45°;(4)
,根据全等三角形的性质求解即可;(3)45°;(4)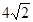
解析试题分析:(1)由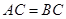 可知此抛物线的对称轴是
可知此抛物线的对称轴是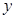 轴,即
轴,即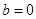 ,即可求得点B、C的坐标,再根据三角形的面积公式求解即可;
,即可求得点B、C的坐标,再根据三角形的面积公式求解即可;
(2)由(1)得点B、C的坐标,即可得到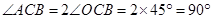 ,证得
,证得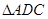 ≌
≌ ,根据全等三角形的性质求解即可;
,根据全等三角形的性质求解即可;
(3)作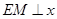 轴,交
轴,交 于点
于点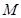 ,易证
,易证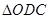 ≌
≌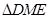 ,所以
,所以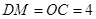 ,
, ,又因为
,又因为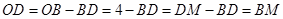 ,即得
,即得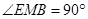 ,从而可以求得结果;
,从而可以求得结果;
(4)由(3)知,点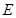 在定直线上,当
在定直线上,当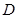 点沿
点沿 轴正方向移动到点
轴正方向移动到点 时,即得点
时,即得点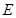 所走过的路线长.
所走过的路线长.
(1)由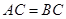 ,可知此抛物线的对称轴是
,可知此抛物线的对称轴是 轴,即
轴,即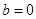
所以
由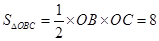 ,得
,得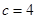
抛物线解析式为 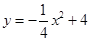 ;
;
(2)由(1)得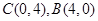
所以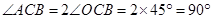
在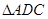 和
和 中
中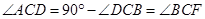 ,
,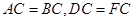
所以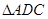 ≌
≌
所以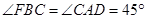
所以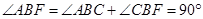
所以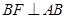 ;
;
(3)作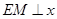 轴,交
轴,交 于点
于点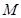
易证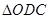 ≌
≌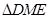
所以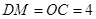 ,
,
又因为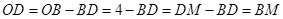
所以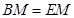
因为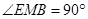
所以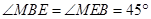 ;
;
(4)由(3)知,点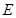 在定直线上
在定直线上
当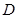 点沿
点沿 轴正方向移动到点
轴正方向移动到点 时,
时,
点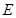 所走过的路线长等于
所走过的路线长等于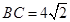 .
.
考点:动点问题的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.


科目:初中数学 来源: 题型:
已知关于x的方程 ![]() .
.
(1)求证: 不论m为任何实数, 此方程总有实数根;
(2)若抛物线![]() 与
与![]() 轴交于两个不同的整数点,且
轴交于两个不同的整数点,且![]() 为正整数,试确定此抛物线的解析式;
为正整数,试确定此抛物线的解析式;
(3)若点P![]() 与Q
与Q![]() 在(2)中抛物线上 (点P、Q不重合), 且y1=y2, 求代
在(2)中抛物线上 (点P、Q不重合), 且y1=y2, 求代
数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
如图,已知抛物线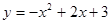 与
与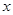 轴的两个交点为A、B,与
轴的两个交点为A、B,与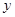 轴交于点C
轴交于点C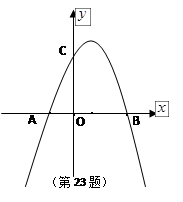
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
查看答案和解析>>
科目:初中数学 来源:2011届河南省周口市初三下学期第二十八章二次函数图像与性质检测题 题型:解答题
已知关于 的方程
的方程 .
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于4且小于8,求m的取值范围;
(3)设抛物线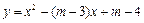 与
与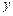 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求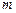 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012年沪科版初中数学九年级上23.4二次函数与一元二次方程练习卷(解析版) 题型:解答题
已知抛物线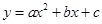 与
与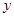 轴交于
轴交于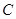 点,与
点,与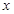 轴交于
轴交于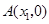 ,
,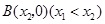 两点,顶点
两点,顶点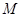 的纵坐标为
的纵坐标为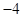 ,若
,若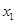 ,
, 是方程
是方程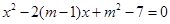 的两根,且
的两根,且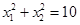 .
.
(1)求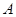 ,
,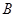 两点坐标;
两点坐标;
(2)求抛物线表达式及点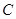 坐标;
坐标;
(3)在抛物线上是否存在着点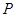 ,使△
,使△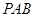 面积等于四边形
面积等于四边形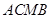 面积的2倍,若存在,求出
面积的2倍,若存在,求出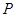 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省周口市初三下学期第二十八章二次函数图像与性质检测题 题型:解答题
已知关于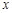 的方程
的方程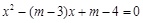 .
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于4且小于8,求m的取值范围;
(3)设抛物线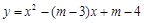 与
与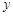 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线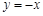 的对称点恰好是点M,求
的对称点恰好是点M,求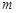 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com