
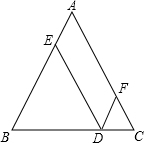
 如图,在△ABC中,AB=AC=10,点D在BC上,DE∥AC交AB于E,DF∥AB交AC于F,求:四边形AEDF的周长.
如图,在△ABC中,AB=AC=10,点D在BC上,DE∥AC交AB于E,DF∥AB交AC于F,求:四边形AEDF的周长. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有些规律问题可以借助函数思想建立数学模型来探讨解决,如此“问题情境”:用同样大小的黑色棋子按如图所示的规律摆放,则第1000个图中共有多少枚棋子?
有些规律问题可以借助函数思想建立数学模型来探讨解决,如此“问题情境”:用同样大小的黑色棋子按如图所示的规律摆放,则第1000个图中共有多少枚棋子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com