练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知的三个顶点的坐标分别为、、，是的边上一点.

    （1）将绕原点逆时针旋转得到，请在网格中画出；

    （2）将沿一定的方向平移后，点的对应点为，请在网格中画出上述平移后的，并写出点的坐标：（ ）；

    （3）若以点为位似中心，作与成的位似，则与点对应的点位似坐标为______（不用作图，直接写出结果）.

    【答案】（1）见解析；（2）见解析，；（3）或

    【解析】

    （1）将绕原点逆时针旋转后的对应点画出来，顺次连接起来，即可；

    （2）根据将沿一定的方向平移后，点的对应点为，可知，先向右平移6个单位，再向上平移2个单位，即可得到；

    （3）根据平面直角坐标系中，以原点为位似中心的位似图形的对应点坐标之比等于相似比，即可得到答案．

    （1）如图所示；

    （2）如图所示，；

    （3）∵以点为位似中心，作与成的位似，

    ∴或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2016年3月国际风筝节期间，王大伯决定销售一批风筝，经市场调研：蝙蝠型风筝进价每个为10元，当售价每个为12元时，销售量为180个，若售价每提高1元，销售量就会减少10个，请回答以下问题：

    （1）用表达式表示蝙蝠型风筝销售量y（个）与售价x（元）之间的函数关系（12≤x≤30）；

    （2）王大伯为了让利给顾客，并同时获得840元利润，售价应定为多少？

    （3）当售价定为多少时，王大伯获得利润W最大，最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若抛物线与轴两个交点间的距离为2，称此抛物线为定弦抛物线，已知某定弦抛物线的对称轴为直线，将此抛物线向左平移2个单位，再向下平移3个单位，得到的抛物线过点( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

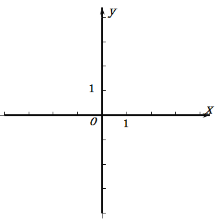
    【题目】已知平面直角坐标系xOy（如图1），一次函数的图像与y轴交于点A，点M在正比例函数的图像上，且MO＝MA．二次函数y＝x2＋bx＋c的图像经过点A、M．

    （1）求线段AM的长；

    （2）求这个二次函数的解析式；

    （3）如果点B在y轴上，且位于点A下方，点C在上述二次函数的图像上，点D在一次函数的图像上，且四边形ABCD是菱形，求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

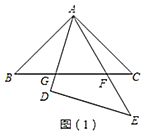
    【题目】如图，在同一平面内，将两个全等的等腰直角三角形和摆放在一起，为公共顶点，，它们的斜边长为2，若固定不动，绕点旋转，、与边的交点分别为、（点不与点重合，点不与点重合），设，．

    （1）请在图（1）中找出两对相似但不全等的三角形，并选取其中一对进行证明．

    （2）求与a的函数关系式，直接写出自变量a的取值范围．

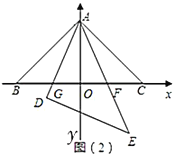
    （3）以的斜边所在的直线为轴，边上的高所在的直线为轴，建立平面直角坐标系如图（2），若，求出点的坐标，猜想线段、和之间的关系，并通过计算加以验证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0 ②4a+2b+c＞0 ③4ac﹣b2＜8a ④＜a＜⑤b＞c．其中含所有正确结论的选项是（　　）

    A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴交于、两点，与轴交于点,抛物线的对称轴为直线，交抛物线于点,交轴于点．

    　　　　　　　　

    （1）求抛物线的函数表达式及点、点的坐标；

    （2）抛物线对称轴上的一动点从点出发，以每秒1个单位的速度向上运动，连接，，设运动时间为秒（），在点的运动过程中，请求出：当为何值时，？

    （3）若点在抛物线上、两点之间运动（点不与点、重合），在运动过程中，设点的横坐标为，的面积为，求关于的函数关系式，并求为何值时有最大值，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，D为边AB上一点，E是CD的中点，且∠ACD＝∠ABE．已知AC＝2，设AB＝x，AD＝y，则y与x满足的关系式为（　　）

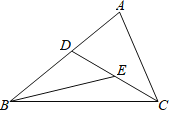
    A.xy＝4B.2xy﹣y2＝4C.xy﹣y2＝4D.x2+xy﹣2y2＝4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

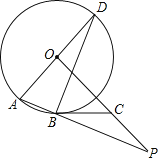
    【题目】如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，点C在OP上，满足∠CBP＝∠ADB．

    （1）求证：BC是⊙O的切线；

    （2）若OA＝2，AB＝1，求线段BP的长．

    查看答案和解析>>

    同步练习册答案