
【题目】如图,在矩形![]() 中,
中,![]() ,点D是边
,点D是边![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过点D,交
的图象经过点D,交![]() 边于点E,直线
边于点E,直线![]() 的解析式为
的解析式为![]() .
.

(1)求反比例函数![]() 的解析式和直线
的解析式和直线![]() 的解析式;
的解析式;
(2)在y轴上找一点P,使![]() 的周长最小,求出此时点P的坐标;
的周长最小,求出此时点P的坐标;
(3)在(2)的条件下,![]() 的周长最小值是______.
的周长最小值是______.
【答案】(1)![]() ,
,![]() ;(2)点P坐标为
;(2)点P坐标为![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先求出D点坐标,然后将D点坐标代入反比例解析式,求出k即可得到反比例函数的解析式.将x=2代入反比例函数解析式求出对应y的值,即得到E点的坐标,然后将点D,E两点的坐标代入一次函数的解析式中,即可求出DE的解析式.
(2)作点D关于y轴的对称点![]() ,连接
,连接![]() ,交y轴于点P,连接
,交y轴于点P,连接![]() .此时
.此时![]() 的周长最小.然后求出
的周长最小.然后求出![]() 直线的解析式,求
直线的解析式,求![]() 直线与y轴的交点坐标,即可得出P点的坐标;
直线与y轴的交点坐标,即可得出P点的坐标;
(3)![]() 的周长的最小值为DE+
的周长的最小值为DE+![]() ,分别利用勾股定理两条线段的长,即可求.
,分别利用勾股定理两条线段的长,即可求.
解:(1)∵D为![]() 的中点,
的中点,![]() ,
,
∴![]() .
.
∵四边形![]() 是矩形,
是矩形,![]() ,
,
∴D点坐标为![]() .
.
∵![]() 在
在![]() 的图象上,
的图象上,
∴![]() .∴反比例函数解析式为
.∴反比例函数解析式为![]() .
.
当![]() 时,
时,![]() .
.
∴E点坐标为![]() .
.
∵直线![]() 过点
过点![]() 和点
和点![]()
∴![]()
解得![]()
∴直线![]() 的解析式为
的解析式为![]() .
.
∴反比例函数解析式为![]() ,
,
直线![]() 的解析式为
的解析式为![]() .
.
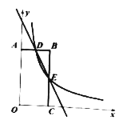
(2)作点D关于y轴的对称点![]() ,连接
,连接![]() ,交y轴于点P,连接
,交y轴于点P,连接![]() .
.
此时![]() 的周长最小.∵点D的坐标为
的周长最小.∵点D的坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
∵直线![]() 经过
经过![]()
∴![]()
解得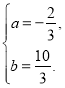
∴直线![]() 的解析式为
的解析式为![]() .
.
令![]() ,得
,得![]() .
.
∴点P坐标为![]() .
.
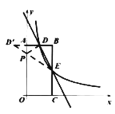
(3)由(1)(2)知D(1,4),E(2,2),![]() (-1,4).又B(2,4),
(-1,4).又B(2,4),
∴BD=1,BE=2,![]() B=3.
B=3.
在Rt△BDE中,由勾股定理,得DE=![]() =
=![]() .
.
在Rt△B![]() E中,由勾股定理,得
E中,由勾股定理,得![]() E=
E=![]() =
=![]() .
.
![]() 的周长的最小值为
的周长的最小值为![]() +DE =
+DE =![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
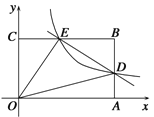
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(6,4).双曲线![]() 经过AB的中点D,且与BC交于点E,连接DE.
经过AB的中点D,且与BC交于点E,连接DE.
(1)求k的值和直线DE的解析式;
(2)若点P是y轴上一点,且△OPE的面积与四边形ODBE的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出某一结果出现的频率折线图.如图所示,则符合这一结果的实验可能是( )
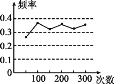
A.抛一枚硬币,出现正面朝上
B.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.掷一个正六面体的骰子,出现3点朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,草原上有A,B,C三个互通公路的奶牛养殖基地,B与C之间距离为100千米,C在B的正北方,A在C的南偏东60°方向且在B的北偏东30°方向.A地每年产奶3万吨;B地有奶牛9000头,平均每头牛的年产奶量为3吨;C地养了三种奶牛,其中黑白花牛的头数占20%,三河牛的头数占35%,其他情况反映在图(2),图(3)中.

(1)通过计算补全图(3);
(2)比较B地与C地中,哪一地平均每头牛的年产奶量更高?
(3)如果从B,C两地中选择一处建设一座工厂解决三个基地的牛奶加工问题,当运送一吨牛奶每千米的费用都为1元,那么从节省运费的角度考虑,应在何处建设工厂?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织了一次全校![]() 名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于
名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于![]() 分,为了更好的了解本次大赛的成绩分布情况,随机抽取了
分,为了更好的了解本次大赛的成绩分布情况,随机抽取了![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行整理,得到下列不完整的统计图表:
分)作为样本进行整理,得到下列不完整的统计图表:
成绩在这![]() 组的数据是:
组的数据是:
![]()
![]()
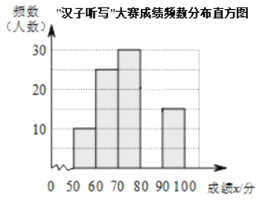
“汉字听写”大赛成绩段频数频率统计表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)表中![]() ,
,![]() ;
;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生获得优胜奖,估计该校参加这次比赛的
分)的学生获得优胜奖,估计该校参加这次比赛的![]() 名学生中获得优胜奖的人数.
名学生中获得优胜奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点.动点
边的中点.动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,同时,动点
运动,同时,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,连接
运动,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 的速度是点
的速度是点![]() 的速度的2倍,在点
的速度的2倍,在点![]() 从点
从点![]() 运动至点
运动至点![]() 的过程中,线段
的过程中,线段![]() 长度的最大值为_________,线段
长度的最大值为_________,线段![]() 长度的最小值为_________.
长度的最小值为_________.
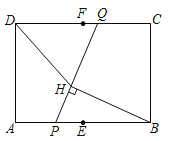
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com