
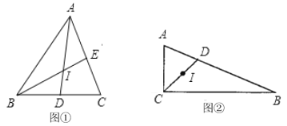
【题目】(1)如图①,小明同学作出![]() 两条角平分线
两条角平分线![]() ,
,![]() 得到交点
得到交点![]() ,就指出若连接
,就指出若连接![]() ,则
,则![]() 平分
平分![]() ,你觉得有道理吗?为什么?
,你觉得有道理吗?为什么?
(2)如图②,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的角平分线
的角平分线![]() 上有一点
上有一点![]() ,设点
,设点![]() 到边
到边![]() 的距离为
的距离为![]() .(
.(![]() 为正实数)
为正实数)
小季、小何同学经过探究,有以下发现:
小季发现:![]() 的最大值为
的最大值为![]() .
.
小何发现:当![]() 时,连接
时,连接![]() ,则
,则![]() 平分
平分![]() .
.
请分别判断小季、小何的发现是否正确?并说明理由.
【答案】(1)有道理,理由详见解析;(2)小季和小何都正确,理由详见解析
【解析】
(1)过I点分别作IM,IN,IK垂直于AB,BC,AC于点M,N,K,根据角平分线的性质即可得解;
(2)根据等积法的相关方法进行求解即可.
(1)如下图,过I点分别作IM,IN,IK垂直于AB,BC,AC于点M,N,K,连接IC
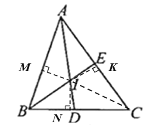
∵AI平分∠BAC,IM⊥AB,IK⊥AC
∴IM=IK,同理IM=IN
∴IK=IN
又∵IK⊥AC,IN⊥BC
∴CI平分∠BCA;
(2)如下图,过C点作CE⊥AB于点E,则d的最大值为CE长
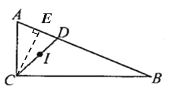
∵![]() ,
,![]()
∴![]()
又∵![]()
∴![]()
∴![]() 的最大值为
的最大值为![]()
∴小季正确;
假设此时![]() 平分
平分![]() ,如下图,连接AI,BI,过I点作IG,IH,IF分别垂直于AC,BC,AB于点G,H,F
,如下图,连接AI,BI,过I点作IG,IH,IF分别垂直于AC,BC,AB于点G,H,F
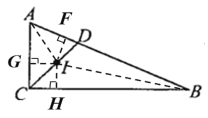
∵AI平分![]() ,CD平分∠ACB
,CD平分∠ACB
∴BI平分∠CBA
∵IG⊥AC,IH⊥BC,ID⊥AB
∴IG=IH=IF=d
∵![]()
∴![]()
∴![]()
∴![]()
∴假设成立,当![]() 时,连接
时,连接![]() ,则
,则![]() 平分
平分![]()
∴小何正确.


科目:初中数学 来源: 题型:
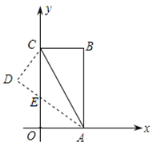
【题目】如图,把长方形纸片![]() 放入平面直角坐标系中,使
放入平面直角坐标系中,使![]() ,
,![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴上,连接
轴上,连接![]() ,将纸片
,将纸片![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 的位置,
的位置,![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
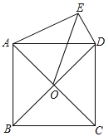
【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8![]() ,则另一直角边AE的长为_____.
,则另一直角边AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生的十次数学竞赛训练成绩的平均分分别是![]() 和
和![]() ,成绩的方差分别是
,成绩的方差分别是![]() 和
和![]() ,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
A. 甲、乙两人平均分相当,选谁都可以
B. 乙的平均分比甲高,选乙
C. 乙的平均分和方差都比甲高,成绩比甲稳定,选乙
D. 两人的平均分相当,甲的方差小,成绩比乙稳定,选甲
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,对角线
,对角线![]() 、
、![]() 相交于点
相交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 顺时针旋转一个角度
顺时针旋转一个角度![]() (
(![]() ),分别交线段
),分别交线段![]() 、
、![]() 于点
于点![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,连接
,连接![]() .
.
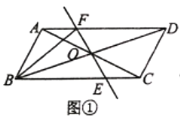

(1)如图①,在旋转的过程中,请写出线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
(2)如图②,当![]() 时,请写出线段
时,请写出线段![]() 与
与![]() 的数量关系,并证明;
的数量关系,并证明;
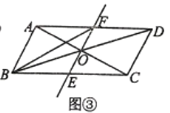
(3)如图③,当![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有
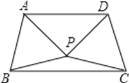
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在元旦节来临之际,小明准备给好朋友赠送一些钢笔和笔记本作为元旦礼物,经调查发现,![]() 支钢笔和
支钢笔和![]() 个笔记本要
个笔记本要![]() 元;
元;![]() 支钢笔和
支钢笔和![]() 个笔记本要
个笔记本要![]() 元.
元.
(1)求一支钢笔和一个笔记本分别要多少元?
(2)小明购买了![]() 支钢笔和
支钢笔和![]() 个笔记本,恰好用完
个笔记本,恰好用完![]() 元钱.若两种物品都要购买,请你帮他设计购买方案.
元钱.若两种物品都要购买,请你帮他设计购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).
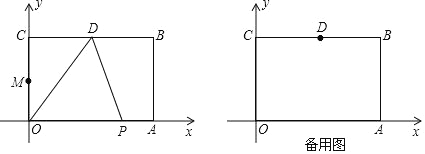
(1)①点D的坐标是(___,___);
②当点P在AB上运动时,点P的坐标是(___,___)(用t表示);
(2)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=___秒.(直接写出参考答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com