
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,若将经过
,若将经过![]() 两点的直线
两点的直线![]() 沿
沿![]() 轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线
轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线![]() .
.
(1)求直线![]() 及抛物线的函数表达式;
及抛物线的函数表达式;
(2)如果P是线段![]() 上一点,设
上一点,设![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,且
,且![]() ,求点P的坐标;
,求点P的坐标;
(3)设![]() 的半径为l,圆心
的半径为l,圆心![]() 在抛物线上运动,则在运动过程中是否存在
在抛物线上运动,则在运动过程中是否存在![]() 与坐标轴相切的情况?若存在,求出圆心
与坐标轴相切的情况?若存在,求出圆心![]() 的坐标;若不存在,请说明理由.并探究:若设⊙Q的半径为
的坐标;若不存在,请说明理由.并探究:若设⊙Q的半径为![]() ,圆心
,圆心![]() 在抛物线上运动,则当
在抛物线上运动,则当![]() 取何值时,⊙Q与两坐轴同时相切?
取何值时,⊙Q与两坐轴同时相切?
 |
(1)解:(1)∵![]() 沿
沿![]() 轴向下平移3个单位后恰好经过原点,
轴向下平移3个单位后恰好经过原点,
∴![]() ,
,![]() 。
。
将![]()
![]() 代入
代入![]() ,得
,得![]() 。解得
。解得![]() 。
。
∴直线AC的函数表达式为![]() 。
。
∵抛物线的对称轴是直线![]()
∴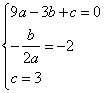 解得
解得![]()
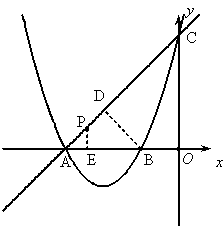 ∴抛物线的函数表达式为
∴抛物线的函数表达式为![]() 。
。
(2)如图,过点B作BD⊥AC于点D。
∵![]() ,
,
∴![]()
∴![]() 。
。
过点P作PE⊥x轴于点E,
∵PE∥CO,∴△APE∽△ACO,
∴![]() ,
,
∴![]()
∴![]() ,解得
,解得![]()
∴点P的坐标为![]()
(3)(Ⅰ)假设⊙Q在运动过程中,存在![]() 与坐标轴相切的情况。
与坐标轴相切的情况。
设点Q的坐标为![]() 。
。
① 当⊙Q与y轴相切时,有![]() ,即
,即![]() 。
。
当![]() 时,得
时,得![]() ,∴
,∴![]()
当![]() 时,得
时,得![]() ,∴
,∴![]()
② 当⊙Q与x轴相切时,有![]() ,即
,即![]()
当![]() 时,得
时,得![]() ,即
,即![]() ,解得
,解得![]() ,∴
,∴![]()
当![]() 时,得
时,得![]() ,即
,即![]() ,解得
,解得![]() ,∴
,∴![]() ,
,![]() 。
。
综上所述,存在符合条件的⊙Q,其圆心Q的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(Ⅱ)设点Q的坐标为![]() 。
。
当⊙Q与两坐标轴同时相切时,有![]() 。
。
由![]() ,得
,得![]() ,即
,即![]() ,
,
∵△=![]()
∴此方程无解。
由![]() ,得
,得![]() ,即
,即![]() ,
,
解得![]()
∴当⊙Q的半径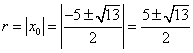 时,⊙Q与两坐标轴同时相切。
时,⊙Q与两坐标轴同时相切。


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com