
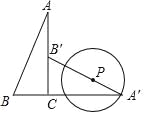
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,AB=13,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为_____.
,AB=13,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为_____.
【答案】![]()
【解析】
先根据直角三角形的性质和勾股定理,结合sinA=513,AC=12求出AB与BC的长,再对⊙P与△ABC相切的位置进行讨论;
①如图1中,当⊙P与直线AC相切于点Q时,连接PQ,根据题意可得PQ∥CA′,从而得到PQCA'=PB'A'B',代入已知条件求出PQ,即为圆的半径;
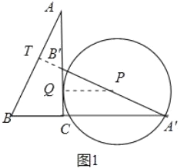
②如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,从而得到△A′BT∽△ABC.利用相似三角形对应边成比例得到A'TAC=A'BAB,求出A′T确定圆的直径,进而求出半径.
∵在△ABC中,∠ACB=90°,sinA=513,AC=12,
∴BC=5,AB=13.
①当⊙P与直线AC相切于点Q时,连接PQ,如图1所示:
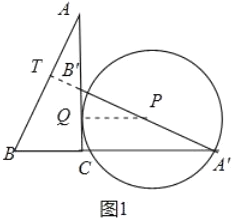
设PQ=PA′=r.
∵PQ∥CA′,
∴PQ:CA'=PB':A'B',
∴r:12=(13r):13,
∴r=![]() .
.
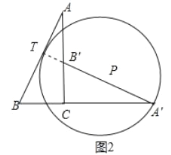
②当⊙P与AB相切于点T时,如图2所示,易证A′、B′、T共线.
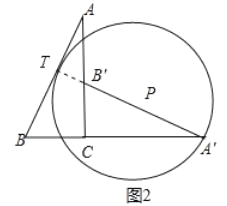
∵△A′BT∽△ABC,
∴A'T:AC=A'B:AB,
∴A'T:12=17:13,
∴A′T=![]() ,
,
∴r=![]() A′T=
A′T=![]() .
.
综上所述,⊙P的半径为![]() .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
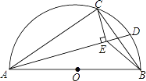
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
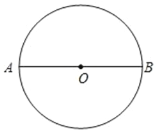
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() 的三个顶点在坐标轴上,
的三个顶点在坐标轴上,![]() ,且
,且![]() ,将
,将![]() 沿着
沿着![]() 翻折到
翻折到![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以
轴以![]() 个单位秒的速度向终点
个单位秒的速度向终点![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,分别交直线
轴,分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒,求
秒,求![]() 与
与![]() 的关系式,并写出
的关系式,并写出![]() 的取值范围.
的取值范围.
(3如图2在(2)的条件下,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 值和点
值和点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地质公园中有两座相邻小山.游客需从左侧小山山脚E处乘坐竖直观光电梯上行100米到达山顶C处,然后既可以沿水平观光桥步行到景点P处,也可以通过滑行索道到达景点Q处,在山顶C处观测坡底A的俯角为75°,观测Q处的俯角为30°,已知右侧小山的坡角为30°(图中的点C,E,A,B,P,Q均在同一平面内,点A,Q,P在同一直线上)
(1)求∠CAP的度数及CP的长度;
(2)求P,Q两点之间的距离.(结果保留根号)
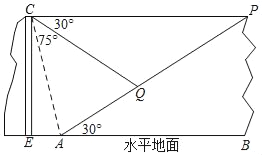
查看答案和解析>>
科目:初中数学 来源: 题型:
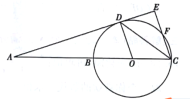
【题目】如图,点D是⊙O上一点,直线AE经过点D,直线AB经过圆心O,交⊙O于B,C两点,CE⊥AE,垂足为点E,交⊙O于点F,∠BCD=∠DCF
(1)求∠A+∠BOD的度数;
(2)若sin∠DCE=![]() ,⊙O的半径为5,求线段AB的长.
,⊙O的半径为5,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接:“国家卫生城市”复检,某市环卫局准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费w(元)与A型垃圾箱x(个)之间的函数关系式;
②当买A型垃圾箱多少个时总费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
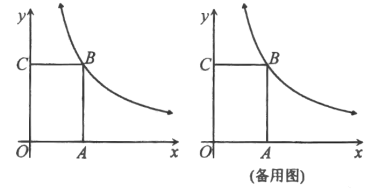
【题目】如图,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com