
 (1)线段AB的长为6cm,延长线段AB到C,使得BC=2AB,取AC的中点D,画出草图并求出BD的长.
(1)线段AB的长为6cm,延长线段AB到C,使得BC=2AB,取AC的中点D,画出草图并求出BD的长.分析 (1)根据题意画出草图,根据线段中点的性质计算即可;
(2)根据邻补角的性质、角平分线的定义进行解答即可.
解答 解:(1)草图如图,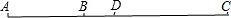 ∵AB=6cm,BC=2AB,
∵AB=6cm,BC=2AB,
∴BC=12cm,
∴AC=18cm,
∵D是AC的中点,
∴AD=$\frac{1}{2}$AC=9cm,
∴BD=AD-AB=3cm;
(2)∵∠FOC=90°,∠1=38°,
∴∠3=90°-38°=52°,
∴∠AOD=180°-52°=128°,又OE平分∠AOD,
∴∠2=$\frac{1}{2}$∠AOD=64°.
点评 本题考查的是对顶角、邻补角的概念和性质、角平分线的定义、两点间的距离的计算,掌握对顶角相等、邻补角之和等于180°是解题的关键,注意数形结合思想在求两点间的距离中的应用.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 过一点有一条直线 | D. | 过一点有无数条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com