
【题目】在农业技术部门指导下,小明家今年种植的猕猴桃喜获丰收.去年猕猴桃的收入结余12000元,今年猕猴桃的收入比去年增加了20%,支出减少10%,结余今年预计比去年多11400元.请计算:
(1)今年结余 元;
(2)若设去年的收入为![]() 元,支出为
元,支出为![]() 元,则今年的收入为 元,支出为 元(以上两空用含
元,则今年的收入为 元,支出为 元(以上两空用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(3)列方程组计算小明家今年种植猕猴桃的收入和支出.
【答案】(1)23400元;(2)今年的收入为:![]() 元,支出为:
元,支出为:![]() 元,(3)小明家今年种植猕猴桃的收入和支出分别为50400元、27000元.
元,(3)小明家今年种植猕猴桃的收入和支出分别为50400元、27000元.
【解析】
(1)根据去年猕猴桃的收入结余12000元,结余今年预计比去年多11400元,可以计算出今年的结余;
(2)根据今年猕猴桃的收入比去年增加了20%,支出减少10%,可以表示出今年的收入和支出;
(3)根据题意可以得到相应的方程组,从而可以求得小明家今年种植猕猴桃的收入和支出.
(1)由题意可得,
今年结余:![]() (元),
(元),
(2)由题意可得,
今年的收入为:![]() (元),
(元),
支出为:![]() (元),
(元),
(3)由题意可得,
![]()
解得![]()
则![]() ,
,
![]() ,
,
答:小明家今年种植猕猴桃的收入和支出分别为50400元、27000元.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】有5张背面看上去无差别的扑克牌,正面分别写着5,6,7,8,9,洗匀后正面向下放在桌子上,从中随机抽取2张,抽出的卡片上的数字恰好是两个连续整数的概率是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为(3,4),
的坐标为(3,4),![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,点
,点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向运动,
轴正方向运动,![]() 与直线
与直线![]() 交于
交于![]() ,则
,则![]() 的面积( )
的面积( )
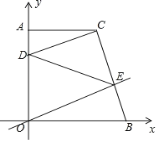
A.逐渐变大B.先变大后变小C.逐渐变小D.始终不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地在城区美化工程招标时,有甲、乙两个工程队投标.经测算,获得以下信息:
信息1:乙队单独完成这项工程需要60天;
信息2:若先由甲、乙两队合做16天,剩下的工程再由乙队单独做20天可以完成;
信息3:甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.
根据以上信息,解答下列问题:
(1)甲队单独完成这项工程需要多少天?
(2)若该工程计划在50天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标中,四边形OABC是梯形,且AB = OC = 4,CB∥OA,OA = 7,∠COA = 60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D,
(1)求点B的坐标;
(2)当点P运动什么位置时,使得∠CPD =∠OAB,且![]() ,求这时点P的坐标;
,求这时点P的坐标;
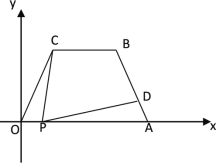
(3)当点P运动什么位置时,△OCP为等腰三角形,直接写出这时点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在画有方格图的平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)将△ACB绕点B顺时针方向旋转![]() ,在方格图中用直尺画出旋转后对应的△A1C1B,则A1点的坐标是(_________),C1点的坐标是(_________).
,在方格图中用直尺画出旋转后对应的△A1C1B,则A1点的坐标是(_________),C1点的坐标是(_________).
(2)在方格图中用直尺画出△ACB关于原点O的中心对称图形△A2C2B2,则A2点的坐标是(_________),C2点的坐标是(_________).

查看答案和解析>>
科目:初中数学 来源: 题型:
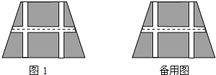
【题目】如图,要设计一个等腰梯形的花坛,花坛上底![]() 米,下底
米,下底![]() 米,上下底相距
米,上下底相距![]() 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为![]() 米.
米.
![]() 用含
用含![]() 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
![]() 当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
![]() 根据设计的要求,甬道的宽不能超过
根据设计的要求,甬道的宽不能超过![]() 米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是
米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是![]() ,花坛其余部分的绿化费用为每平方米
,花坛其余部分的绿化费用为每平方米![]() 万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
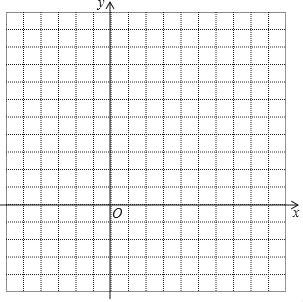
【题目】二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数y=x2+bx+c的图象.
(4)写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
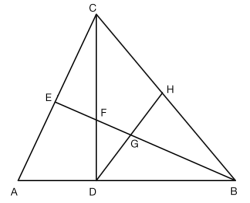
【题目】如图,![]() 是
是![]() 的两条高线,且它们相交于
的两条高线,且它们相交于![]() 是
是![]() 边的中点,连结
边的中点,连结![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,已知
,已知![]() .
.
(1)求证BF=AC.
(2)若BE平分![]() .
.
①求证:DF=DG.
②若AC=8,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com