
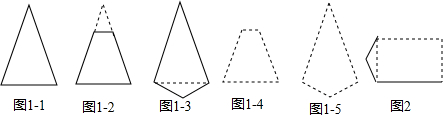
分析 (1)根据等腰三角形的性质、矩形的性质以及等边三角形的性质进行判断即可;
(2)中图1-2和图1-3都可以看作由图1-1修改得到的,在图1-4和图1-5中,分别仿照类似的修改方式进行画图即可;
(3)长方形具有两条对称轴,在长方形的右侧补出与左侧一样的图形,即可构造出一个恰好有2条对称轴的凸六边形;
(4)在等边三角形的基础上加以修改,即可得到恰好有3条对称轴的凸六边形.
解答 解:(1)非等边的等腰三角形有1条对称轴,非正方形的长方形有2条对称轴,等边三角形有3条对称轴,
故答案为:1,2,3;
(2)恰好有1条对称轴的凸五边形如图中所示.
(3)恰好有2条对称轴的凸六边形如图所示.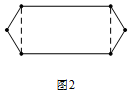
(4)恰好有3条对称轴的凸六边形如图所示.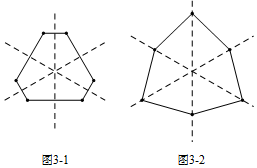
点评 本题属于四边形综合题,主要考查了轴对称图形的性质,解决问题的关键是掌握等腰三角形的性质,矩形的性质以及等边三角形的性质.轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.常见的轴对称图形有:等腰三角形,矩形,正方形,等腰梯形,圆等等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+1)2+1 | B. | y=(x-3)2+1 | C. | y=(x-3)2-5 | D. | y=(x+1)2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
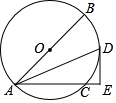 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1(精确到0.1) | B. | 0.05(精确到0.01) | ||
| C. | 0.05(精确到0.001) | D. | 0.0503(精确到0.0001) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-6 | B. | m>-6且m≠0 | C. | m>-6且m≠-4 | D. | m>-6且m≠2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com