
���� ��1���ٸ��ݶ����������T���г���Ԫһ�η����飬�ⷽ�������a��b��ֵ��
�ڸ��ݣ�1�������a��b��ֵ���������г����������m��ȡֵ��Χ�����������г�����ʽ���ⲻ��ʽ���ʵ��p��ȡֵ��Χ��
��2�������������г���ʽ������x��y��ϵ��Ϊ0�����a��bӦ����Ĺ�ϵʽ��
��� �⣺��1����$\left\{\begin{array}{l}{a-2b-1=-2}\\{4a+4b-1=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{2}{3}}\end{array}\right.$��
��$\left\{\begin{array}{l}{\frac{2m}{3}+\frac{4��5-4m��}{3}-1��4}\\{\frac{m}{3}+\frac{4��3-2m��}{3}-1��p}\end{array}\right.$��
���$\frac{5}{14}$��m��$\frac{9-3p}{7}$��
��Ϊԭ����ʽ����2�������⣬
����2��$\frac{9-3p}{7}$��3��
��ã�-4��p��-$\frac{5}{3}$��
��2��T��x��y��=ax+2by-1��T��y��x��=ay+2bx-1��
����ax+2by-1=ay+2bx-1��
���ԣ�a-2b����x-y��=0
����a=2b��
���� ���⿼����Ƕ�Ԫһ�η�����Ľⷨ��һԪһ�β���ʽ��Ľⷨ��һԪһ�β���ʽ����������ȷ�������ն�Ԫһ�η�����Ľⷨ��һԪһ�β���ʽ��Ľⷨ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
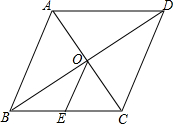 ��ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��AC=6cm��BD=8cm����E�DZ�BC���е㣬����OE����OE=2.5cm��
��ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��AC=6cm��BD=8cm����E�DZ�BC���е㣬����OE����OE=2.5cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
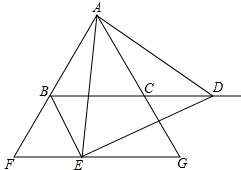 ��ͼ����ABC�ǵȱ������Σ���D������BC�ϵ�һ�����㣨��D�����B��C�غϣ�����ADE����ADΪ�ߵĵȱ������Σ�����E��BC��ƽ���ߣ��ֱ�����AB��AC�ڵ�F��G������BE��
��ͼ����ABC�ǵȱ������Σ���D������BC�ϵ�һ�����㣨��D�����B��C�غϣ�����ADE����ADΪ�ߵĵȱ������Σ�����E��BC��ƽ���ߣ��ֱ�����AB��AC�ڵ�F��G������BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��2 | B�� | 2��4 | C�� | -4��-2 | D�� | -2��-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
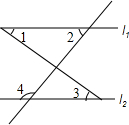 ��ͼ�������ж���ȷ���ǣ�������
��ͼ�������ж���ȷ���ǣ�������| A�� | ����1+��2=180�㣬��l1��l2 | B�� | ����2=��3����l1��l2 | ||
| C�� | ����1+��2+��3=180�㣬��l1��l2 | D�� | ����2+��4=180�㣬��l1��l2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
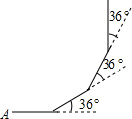 ��ͼ��С����A���������ֱ��ǰ��12������ת36�㣬����ֱ��ǰ��12�ף�������ת36�㡭����������ȥ������һ�λص�������A��ʱ��һ������120�ף�
��ͼ��С����A���������ֱ��ǰ��12������ת36�㣬����ֱ��ǰ��12�ף�������ת36�㡭����������ȥ������һ�λص�������A��ʱ��һ������120�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
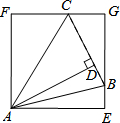 ��ͼ����ABC�У���BAC=45�㣬AD��BC��BD=1��CD=3������ABD��AB�۵��õ���ABE������ACD��AC�۵��õ���ACF���ӳ�EB��FC���ڵ�G��
��ͼ����ABC�У���BAC=45�㣬AD��BC��BD=1��CD=3������ABD��AB�۵��õ���ABE������ACD��AC�۵��õ���ACF���ӳ�EB��FC���ڵ�G���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com