练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
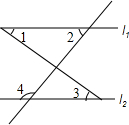
    7．如图，下列判断正确的是（　　）
    A．若∠1+∠2=180°，则l1∥l2B．若∠2=∠3，则l1∥l2
    C．若∠1+∠2+∠3=180°，则l1∥l2D．若∠2+∠4=180°，则l1∥l2

    分析 根据平行线的判定定理对各选项进行逐一判断即可．

    解答 解：A、∠1+∠2=180°与l1∥l2无关，故本选项错误；
    B、∠2=∠3与l1∥l2无关，故本选项错误
    C、∠1+∠2+∠3=180°与l1∥l2无关，故本选项错误；
    D、∵∠2与∠4是同旁内角，∠2+∠4=180°，∴l1∥l2，故本选项正确．
    故选D．

    点评 本题考查的是平行线的判定，用到的知识点为：同旁内角互补，两直线平行．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．计算（$\frac{1}{4}$）-2的结果等于（　　）
    A．-$\frac{1}{8}$B．$\frac{1}{8}$C．-16D．16

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．小明建立了如图的直角坐标系，则点“A“坐标是（　　）
    A．（1，-1）B．（-1，1）C．（-1，2）D．（1，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．不等式组$\left\{\begin{array}{l}{3x-1＞-4}\\{-5x≥-22}\end{array}\right.$的解集中，整数解共有5个．它们分別是0、1、2、3、4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．对x，y定义一种新运算T，规定：T（x，y）=ax+2by-1（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）=a•0+2b•1-1=2b-1．
    （1）已知T（1，-1）=-2，T（4，2）=3．
    ①求a，b的值；
    ②若关于m的不等式组$\left\{\begin{array}{l}{T（2m，5-4m）≤4}\\{T（m，3-2m）＞p}\end{array}\right.$恰好有2个整数解，求实数p的取值范围；
    （2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

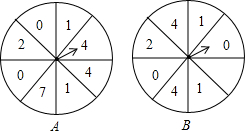    12．某天，小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军．如图，两个可以自由转动的转盘A，B，每个转盘被分成8个相等的扇形，其规则如下：①小明自由转动转盘A，同时小华自由转动转盘B；②转盘停止后，指针指向几就顺时针走几格，得到一个数字（若转盘A中指针指向2，则按顺时针方向走2格得到数字1）；③若最终得到的数字是1，则自己所支持的球队称为预测冠军（若双方都得到1，则重新开始）．这个游戏对双方公平吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图所示，将正方体沿面AB1C切下，则切下的小几何体为三棱锥．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图所示，抛物线y=ax2+bx+4与x轴交于A，B两点，与y轴交于C点，且A（-2，0）、B（4，0），其原点为D，连接BD，点P是线段BD上的一个动点（不与B、D重合），过点P作y轴的垂线，垂足为E，连接BE．
    （1）求抛物线的解析式，并写出原点D的坐标；
    （2）设P点的坐标为（x，y），△PBE的面积为S，求S与x之间的函数关系式，写出自变量x的取值范围，并求出S的最大值；
    （3）在（2）的条件下，当S取值最大值时，过点P作x轴的垂线，垂足为F，连接EF，△PEF沿直线EF折叠，点P的对应点为点P′，请直接写出P′点的坐标，并判断点P′是否在该抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

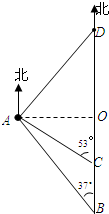    13．如图，一艘货船以每小时48海里的速度从港口B出发，沿正北方向航行．在港口B处时，测得灯塔A处在B处的北偏西37°方向上，航行至C处，测得A处在C处的北偏西53°方向上，且A、C之间的距离是45海里．在货船航行的过程中，求货船与灯塔A之间的最短距离及B、C之间的距离；若货船从港口B出发2小时后到达D，求A、D之间的距离．
    （参考数据：sin53°≈$\frac{4}{5}$，cos53°≈$\frac{3}{5}$，tan53°≈$\frac{4}{3}$）

    查看答案和解析>>

    同步练习册答案