
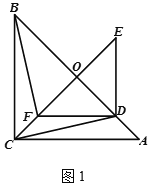
【题目】阅读材料:如图![]() ,
,![]() 与
与![]() 都是等腰直角三角形
都是等腰直角三角形![]() ,且点
,且点![]() 在
在![]() 边上,
边上,![]() ,
,![]() 的中点均为
的中点均为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,显然,点
,显然,点![]() ,
,![]() ,
,![]() 在同一条直线上,可以证明
在同一条直线上,可以证明![]() ,所以
,所以![]()
解决问题:
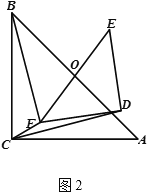
(1) 将图![]() 中的
中的![]() 绕点
绕点![]() 旋转到图
旋转到图![]() 的位置, 猜想此时线段
的位置, 猜想此时线段![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
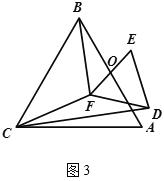
(2) 如图![]() ,若
,若![]() 与
与![]() 都是等边三角形,
都是等边三角形,![]() ,
,![]() 的中点均为
的中点均为![]() ,上述
,上述![]() 中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出
中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
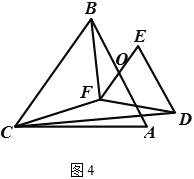
(3) 如图![]() , 若
, 若![]() 与
与![]() 都是等腰三角形,
都是等腰三角形,![]() ,
,![]() 的中点均为
的中点均为![]() ,且顶角
,且顶角![]() ,
,![]() 与
与![]() 之间的数量关系如何(用含
之间的数量关系如何(用含![]() 的式子表示出来)?请直接写出结果.
的式子表示出来)?请直接写出结果.
【答案】(1)![]() ,证明见解析;(2)(1)中的结论不成立,为
,证明见解析;(2)(1)中的结论不成立,为![]() ;(3)
;(3)![]()
【解析】
(1)如答图②所示,连接OC、OD,由全等三角形的判定定理SAS证明△BOF≌△COD;
(2)如答图③所示,连接OC、OD,由等边三角形的性质和锐角三角函数的定义推知![]() ,结合∠BOF=∠COD即可证明△BOF∽△COD,相似比为
,结合∠BOF=∠COD即可证明△BOF∽△COD,相似比为![]() ;
;
(3)如答图④所示,连接OC、OD,由等边三角形的性质和锐角三角函数的定义推知![]() ,结合∠BOF=∠COD即可证明△BOF∽△COD,相似比为tan
,结合∠BOF=∠COD即可证明△BOF∽△COD,相似比为tan![]() .
.
解:(1)猜想:![]() ,
,
证明如下:连接![]() ,
,![]() ,如解图
,如解图![]() 所示
所示
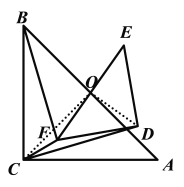
解图1
![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 为斜边
为斜边![]() 的中点,
的中点,
![]() ,
,![]()
![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 为
为![]() 斜边的中点,
斜边的中点,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,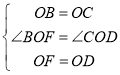 ,
,
![]() ,
,
![]() ;
;
(2)![]() 中的结论不成立
中的结论不成立
连接![]() ,
,![]() ,如解图
,如解图![]() 所示
所示
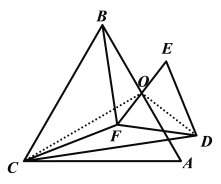
解图2
![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 为斜边
为斜边![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 为
为![]() 斜边的中点,
斜边的中点,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,![]() ,
,![]()
![]()
![]() ;
;
(3)如解图3所示,连接OC、OD, 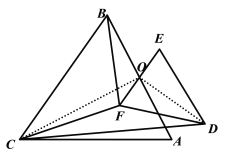
解图3
∵△ABC为等腰三角形,点O为底边AB的中点,
∴![]() ,∠BOC=90°,
,∠BOC=90°,
∵△DEF为等腰三角形,点O为底边EF的中点,
∴![]() ,∠DOF=90°,
,∠DOF=90°,
∴![]() ,
,
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD,
在△BOF与△COD中,
∵![]() ,∠BOF=∠COD,
,∠BOF=∠COD,
∴△BOF∽△COD,
∴![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4),则PDCD的最大值是( ).
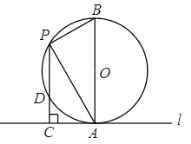
A.2B.3C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过直线![]() 上一点
上一点![]() 作
作![]() 轴于点
轴于点![]() ,线段
,线段![]() 交函数
交函数![]() 的图像于点
的图像于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() .
.
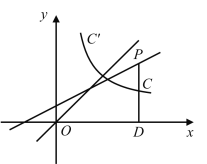
(1)求![]() 、
、![]() 的值;
的值;
(2)求直线![]() 与函数
与函数![]() 图像的交点坐标;
图像的交点坐标;
(3)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
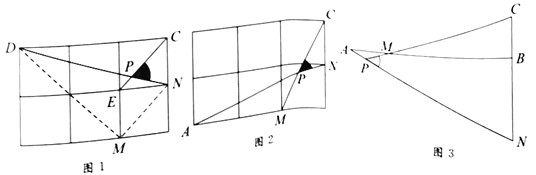
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() , 点
, 点![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 从点
从点![]() 沿折线
沿折线![]() 运动到
运动到![]() 时停止, 点
时停止, 点![]() 从点
从点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,它们运动
时停止,它们运动![]() 的速度都是
的速度都是![]() ,若点
,若点![]() ,
,![]() 同时开始运动, 设运动时间为
同时开始运动, 设运动时间为![]() ,
,![]() 的面积为
的面积为![]() (当
(当![]() ,
,![]() ,
, ![]() 三点共线时,不妨设
三点共线时,不妨设![]() ).已知
).已知![]() 与
与![]() 之间的函数关系的图象如图
之间的函数关系的图象如图![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
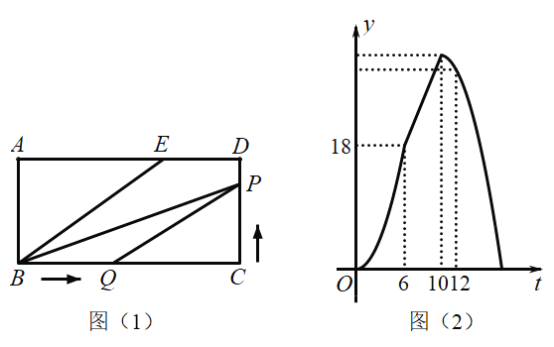
A.![]() B.
B.![]() C.当
C.当![]() 时,
时,![]() D.当
D.当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
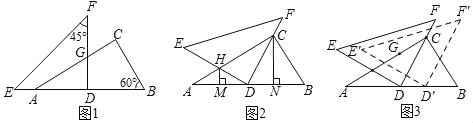
【题目】将一副三角尺按图1摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,![]() .
.
(1)求GC的长;
(2)如图2,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想.
(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】
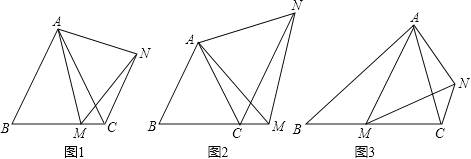
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标为(0,2),点B的坐标为(1,0),连结AB,以AB为边在第一象限内作正方形ABCD,直线BD交双曲线y═![]() (k≠0)于D、E两点,连结CE,交x轴于点F.
(k≠0)于D、E两点,连结CE,交x轴于点F.

(1)求双曲线y=![]() (k≠0)和直线DE的解析式.
(k≠0)和直线DE的解析式.
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打好疫情期间的复工复产攻坚战,某公司决定为员工采购一批口罩和消毒液,经了解,购买4包口罩和3瓶消毒液共需要185元,购买8包口罩和5瓶消毒液共需要335元,
(1)一包口罩和一瓶消毒液各需要多少元?
(2)实际购买时发现厂家有两种优惠方案:方案一:购买口罩不超过20包时,每包都按九折优惠,超过20包时,超过部分每包按七折优惠;方案二:口罩和消毒液都按原价的八折优惠,公司购买![]() 包口罩,10瓶消毒液.
包口罩,10瓶消毒液.
①求两种方案下所需的费用![]() (单位:元)与
(单位:元)与![]() (单位:包)的函数关系式;
(单位:包)的函数关系式;
②若该公司决定购买![]() 包口罩和10瓶消毒液,请你帮助该公司决定选择哪种方案更合算.
包口罩和10瓶消毒液,请你帮助该公司决定选择哪种方案更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com