
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,直线
是抛物线的顶点,直线![]() 是抛物线的对称轴,且点
是抛物线的对称轴,且点![]() 的坐标为
的坐标为![]() .
.
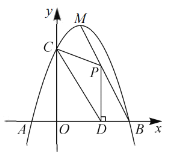
(1)求抛物线的解析式.
(2)已知![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,请求出点
为等腰三角形?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②当
;②当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)点C坐标代入解析式可求c的值,由对称轴可求b的值,即可求解;
(2)①先求出点M,点A,点B的坐标,利用待定系数法可求BM解析式,由三角形的面积公式可求解;
②利用二次函数的性质可求解;
(3)分三种情况讨论,利用两点距离公式列出方程可求解.
(1)![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
又![]() 抛物线与
抛物线与![]() 轴的交点为
轴的交点为![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
(2)①![]() 顶点
顶点![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() 代入,
代入,
得![]() 解得
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
![]() 轴且
轴且![]() ,
,
![]() 的面积
的面积![]() .
.
![]() 点
点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,
![]() ,
,
故![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() .
.
②![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
当![]() 时,
时,![]() 没有最小值.
没有最小值.
综上,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]()
(3)存在.
当![]() 时,
时,
![]() ,
,
![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,此时
,此时![]() .
.
当![]() 时,
时,
![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ,此时
,此时![]() .
.
当![]() 时,
时,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() ,均不符合题意,舍去.
,均不符合题意,舍去.
综上所诉,存在点![]() 使
使![]() 为等腰三角形,点
为等腰三角形,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】为了坚持以人民为中心的发展思想,以不断改善民生为发展的根本目的,某机构随机对某小区部分居民进行了关于“社区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表,根据图标信息,解答下列问题:
满意度 | 人数 | 所占百分比 |
非常满意 | 12 |
|
满意 | 54 |
|
比较满意 |
|
|
不满意 | 6 |
|
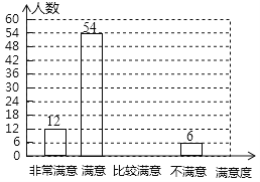
(1)本次调查的总人数为_______.
(2)请补全条形统计图;
(3)据统计,该社区服务站平均每天接待居民约1000名,若将“非常满意”和“消意”作为居民对社区服务站服务工作的肯定,请你估计该社区服务站服务工作平均每天得到多少名居民的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x﹣![]() )(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=
)(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=![]() .
.
(1)求a值;
(2)点P为第一象限内抛物线上一点,点P的横坐标为t,连接PA,PC,设△PAC的面积为S,求S与t之间的关系式;
(3)在(2)的条件下,点Q在第一象限内的抛物线上(点Q在点P的上方),过点P作PE⊥AB,垂足为E,点D在线段AQ上,点F在线段AO上连接ED、DF,DE交AP于点G,若∠QDF+∠QDE=180°,∠DFA+∠AED=90°,PG=PE,PG:EF=3:2,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() .绘画;
.绘画;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演讲;
.演讲;![]() .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
.书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
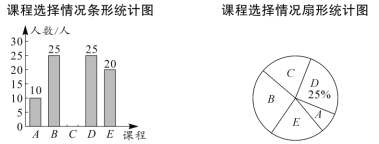
请结合统计图中的信息解决下列问题:
(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整.
(3)求扇形统计图中课程![]() 所对应扇形的圆心角的度数.
所对应扇形的圆心角的度数.
(4)如果该校共有1200名学生,请你估计该校选择课程![]() 的学生约有多少人.
的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年我国个人所得税征收办法最新规定:月收入不超过
年我国个人所得税征收办法最新规定:月收入不超过![]() 元的部分不收税;月收入超过
元的部分不收税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税;月收入超过
的所得税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税
的所得税![]() 国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入
国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入![]() 元,专项附加费支出
元,专项附加费支出![]() 元,他应缴纳个人所得税为:
元,他应缴纳个人所得税为:![]() (元).
(元).
(1)当月收入超过![]() 元而又不超过
元而又不超过![]() 元时,写出应缴纳个人所得税
元时,写出应缴纳个人所得税![]() (元)与月收入
(元)与月收入![]() (元)之间的关系式;
(元)之间的关系式;
(2)如果某人当月专项附加费支出![]() 元,缴纳个人所得税
元,缴纳个人所得税![]() 元,那么此人本月工资是多少元?
元,那么此人本月工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一颗古树BH和教学楼CG的高,先在A处用高1.5米的测角仪AF测得古树顶端H的仰角∠HFE为45°,此时教学楼顶端G恰好在视线FH上,再向前走10米到达B处,又测得教学楼顶端G的仰角∠GED为60°,点A、B、C三点在同一水平线上.求教学楼CG的高.(参考数据:![]() 1.4,
1.4,![]() 1.7)
1.7)
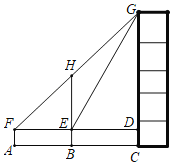
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建成学校举行美化绿化校园活动,九年级计划购买![]() ,
,![]() 两种花木共100棵绿化操场,其中
两种花木共100棵绿化操场,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若购进![]() ,
,![]() 两种花木刚好用去8000元,则购买了
两种花木刚好用去8000元,则购买了![]() 两种花木各多少棵?
两种花木各多少棵?
(2)如果购买![]() 花木的数量不少于
花木的数量不少于![]() 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com