
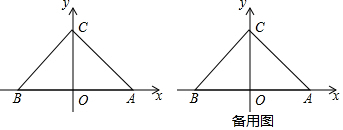
���� ��1����������õ�OC��ֱƽ��AB������ֱ�������ε����ʵõ�OA=OC=5���õ��𰸣�
��2����PD��OC�ڵ�D��֤����PDC�ա�CEQ������ȫ�������ε����ʽ��
��3���������⻭��ͼ�Σ����ݡ�PDC�ա�CEQ���õ�QE=CD=2t������QM=6HN�г���ϵʽ�����㼴�ɣ�
��� �⣺��1����B����A�����y��Գƣ�C����y���ϣ�
��OC��ֱƽ��AB��
��AC=BC��
�ߡ�ACB=90�㣬
���CBA=��CAB=45�㣬
�ߡ�AOC=90�㣬
���CAB=��ACO=45�㣬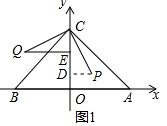
��OA=OC��
��A���������5��0��
��OA=OC=5��
��C��0��5����
��2����PD��OC�ڵ�D��
��QE��OC��PD��OC��
���QEC=��PDC=90�㣬
��P��t��-2t+5����
��PD=t��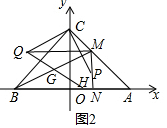
�ߡ�PCQ=90�㣬
���PCD+��QCE=90�㣬
�ߡ�PDC=90�㣬
���PCD+��P=90�㣬
���QCE=��P��
��PC=CQ����QEC=��PDC=90�㣬
���PDC�ա�CEQ��
��CE=PD=t��
��OC=5��
��OE=5-t��
��3����P��t��-2t+5����
��OD=-2t+5��
��OC=5��
��CD=2t��
�ɣ�2��֪��PDC�ա�CEQ��
��QE=CD=2t��
��OE=5-t��Q��-2t��5-t����
��QE��OC��
���CEM=90�㣬
�ߡ�ACO=45�㣬
���CME=��ACO=45�㣬
��CE=EM=t��
��M��t��5-t����
��P��t��-2t+5����
��PM��y�ᣬN��t��0����PM=��5-t��-��-2t+5��=t��
��G��BM���е㣬
��BG=GM��
��QE��OC��
���QEC=��BOC=90�㣬
��QM��BN��
���QMB=��HBM��
�ߡ�BGH=��MGQ��
���QGM�ա�HGB��
��BH=QM=2t+t=3t��
��B����A�����y��Գƣ�A�������Ϊ��5��0����
��B��-5��0����
��N��t��0����
��NB=t+5��
��HN=5-2t��
��QM=6HN��
��3t=6��5-2t����
��t=2��
��PM=2��
���� ���⿼����Ǽ��α任���ۺ�Ӧ�ã�������ԳƵ����ʡ���ת�任�����ʡ�ȫ�������ε��ж����������ʶ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.24��103 | B�� | 2.4��106 | C�� | 2.4��105 | D�� | 24��104 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
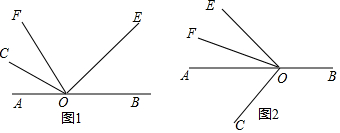
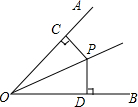 ��ͼ��OPΪ��AOB�Ľ�ƽ���ߣ�PC��OA��PD��OB������ֱ���C��D�������н��۴�����ǣ�������
��ͼ��OPΪ��AOB�Ľ�ƽ���ߣ�PC��OA��PD��OB������ֱ���C��D�������н��۴�����ǣ�������| A�� | PC=PD | B�� | OC=OD | C�� | ��CPO=��DPO | D�� | ��CPD=��DOC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $sin{60��}=\frac{1}{2}$ | B�� | $tan{60��}=\sqrt{3}$ | C�� | $sin{45��}=\frac{{\sqrt{3}}}{2}$ | D�� | $cos{30��}=\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com