
| A. | (-1,2) | B. | (1,-2) | C. | (-1,-2) | D. | (1,2) |
分析 首先得出P点坐标,再根据题意画出P的对称点P′,过P′作P′N⊥y轴于N,过P作PM⊥x轴于M,得出△POM≌△P′ON,推出P′N=PM,ON=OM,根据P的坐标即可求出答案.
解答 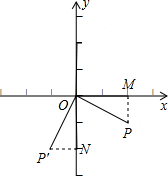 解:∵点A(a,1)与B(-2,b)关于坐标原点对称,
解:∵点A(a,1)与B(-2,b)关于坐标原点对称,
∴a=2,b=-1,
∴P点坐标为:(2,-1),
以直角坐标系原点为中心,将点P(2,-1)顺时针旋转90°后到P′点,
过P′作P′N⊥y轴于N,过P作PM⊥x轴于M,
则OP=OP′,∠P′OP=90°,∠P′NO=∠PMO=90°,
在△P′ON和△POM中
$\left\{\begin{array}{l}{∠PMO=∠P′NO}\\{∠MOP=∠NOP′}\\{OP=OP′}\end{array}\right.$,
∴△POM≌△P′ON(AAS),
∴P′N=PM,ON=OM,
∵P(2,-1),
∴OM=2,PM=1,
∴P′(-1,-2).
故选:C.
点评 本题主要考查对坐标与图形变换-旋转,全等三角形的性质和判定等知识点的理解和掌握,能正确画出图形并求出△POM≌△P′ON是解此题的关键.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.
某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
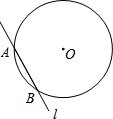 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{π}{2}$+$\sqrt{3}$ | D. | $\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com