
【题目】已知函数f(t)= ![]() ,g(x)=cosxf(sinx)﹣sinxf(cosx),x∈(π,
,g(x)=cosxf(sinx)﹣sinxf(cosx),x∈(π, ![]() ).
).
(1)求函数g(x)的值域;
(2)若函数y=|cos(ωx+ ![]() )|f(sin(ωx+
)|f(sin(ωx+ ![]() ))(ω>0)在区间[
))(ω>0)在区间[ ![]() ,π]上为增函数,求实数ω的取值范围.
,π]上为增函数,求实数ω的取值范围.
【答案】
(1)解: ![]() ,∵
,∵ ![]()
∴ ![]() ,∴cosxf(sinx)=﹣1﹣sinx
,∴cosxf(sinx)=﹣1﹣sinx
同理sinxf(cosx)=﹣1﹣cosx,∴ ![]()
∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]()
∴ ![]()
(2)解:由(1) 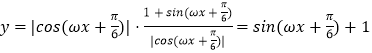
∵ ![]() ,
, ![]() ,∴
,∴ ![]()
令 ![]() ,k∈Z;解之得
,k∈Z;解之得 ![]() ,k∈Z
,k∈Z
则y=|cos(ωx+ ![]() )|f(sin(ωx+
)|f(sin(ωx+ ![]() ))(ω>0)的单调递增区间为
))(ω>0)的单调递增区间为 ![]() ,k∈Z,
,k∈Z,
由已知函数y=|cos(ωx+ ![]() )|f(sin(ωx+
)|f(sin(ωx+ ![]() ))(ω>0)在区间[
))(ω>0)在区间[ ![]() ,π]上为增函数,
,π]上为增函数,
解之得 ![]() ,
,
∵ ![]() ,∴k=0,∴
,∴k=0,∴ ![]()
【解析】(1)求出函数g(x),利用辅助角公式化简,即可求函数g(x)的值域;(2)求出y=|cos(ωx+ ![]() )|f(sin(ωx+
)|f(sin(ωx+ ![]() ))(ω>0)的单调递增区间为
))(ω>0)的单调递增区间为 ![]() ,k∈Z,利用函数y=|cos(ωx+
,k∈Z,利用函数y=|cos(ωx+ ![]() )|f(sin(ωx+
)|f(sin(ωx+ ![]() ))(ω>0)在区间[
))(ω>0)在区间[ ![]() ,π]上为增函数,求实数ω的取值范围.
,π]上为增函数,求实数ω的取值范围.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则cosAcosB=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣5,4),
=(﹣5,4), ![]() =(1﹣λ,3λ+2).
=(1﹣λ,3λ+2).
(1)若△ABC为直角三角形,且∠B为直角,求实数λ的值;
(2)若点A、B、C能构成三角形,求实数λ应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() ,则下列命题中正确命题的序号是 .
,则下列命题中正确命题的序号是 .
①f(x)是偶函数;
②f(x)的值域是[ ![]() ,2];
,2];
③当x∈[0, ![]() ]时,f(x)单调递增;
]时,f(x)单调递增;
④当且仅当x=2kπ± ![]() (k∈Z)时,f(x)=
(k∈Z)时,f(x)= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
(Ⅰ) 求证:PC⊥AD;
(Ⅱ) 在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由;
(Ⅲ) 求点D到平面PAM的距离. 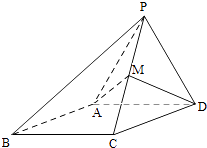
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( ) 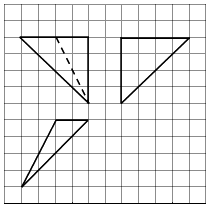
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2﹣n,数列{bn}的前n项和Tn=4﹣bn .
(1)求数列{an}和{bn}的通项公式;
(2)设cn= ![]() anbn , 求数列{cn}的前n项和Rn的表达式.
anbn , 求数列{cn}的前n项和Rn的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com