
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
.
(Ⅰ)求证:平面PAM⊥平面PDM;
(Ⅱ)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.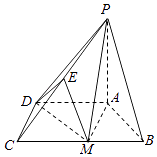
【答案】解:(Ⅰ)证明:∵△ABM是边长为2的等边三角形,底面ABCD是直角梯形,∴ ![]() , 又
, 又 ![]() ,∴CM=3,∴AD=3+1=4,∴AD2=DM2+AM2 , ∴DM⊥AM.
,∴CM=3,∴AD=3+1=4,∴AD2=DM2+AM2 , ∴DM⊥AM.
又PA⊥底面ABCD,∴DM⊥PA,∴DM⊥平面PAM,
∵DM平面PDM,∴平面PAM⊥平面PDM.
(Ⅱ)以D为原点,DC所在直线为x轴,DA所在直线为y轴,
过D且与PA平行的直线为z轴,建立空间直角坐标系D﹣xyz,
则 ![]() ,
, ![]() ,
, ![]() ,
,
设平面PMD的法向量为 ![]() ,
,
则  ,
,
取x1=3,∴ ![]() .
.
∵E为PC中点,则  ,
,
设平面MDE的法向量为 ![]() ,
,
则  ,取x2=3,∴
,取x2=3,∴ ![]() .
.
由  .
.
∴二面角P﹣MD﹣E的余弦值为 ![]()
【解析】(Ⅰ)证明DM⊥AM.DM⊥PA,推出DM⊥平面PAM,即可证明平面PAM⊥平面PDM.(Ⅱ)以D为原点,DC所在直线为x轴,DA所在直线为y轴,过D且与PA平行的直线为z轴,建立空间直角坐标系D﹣xyz,求出平面PMD的法向量,平面MDE的法向量,利用向量的 数量积求解二面角P﹣MD﹣E的余弦值.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图. 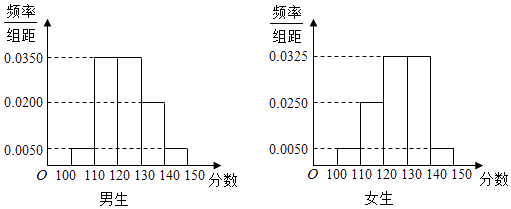
附:K2= ![]() .
.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
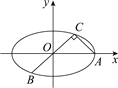
【题目】已知A,B,C是椭圆C: ![]() (a>b>0)上的三点,其中点A的坐标为(2
(a>b>0)上的三点,其中点A的坐标为(2![]() ,0),BC过椭圆的中心,且
,0),BC过椭圆的中心,且![]() ·
·![]() =0,|
=0,|![]() |=2|
|=2|![]() |
|
(1)求椭圆C的方程;
(2)过点(0,t)的直线l(斜率存在)与椭圆C交于P,Q两点,设D为椭圆C与y轴负半轴的交点,且|![]() |=|
|=|![]() |,求实数t的取值范围.
|,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
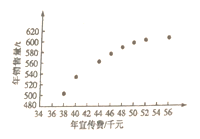
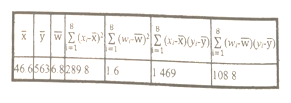
表中![]() .
.
(1)根据散点图判断![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归类型?(给出判断即可,不必说明理由)
的回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的利润![]() 与
与![]() 的的关系为
的的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
(ⅰ)年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的的斜率和截距的最小二乘估计为
的的斜率和截距的最小二乘估计为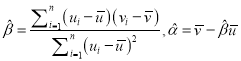 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列叙述: ①若α,β均为第一象限,且α>β,则sinα>sinβ
②函数f(x)=sin(2x﹣ ![]() )在区间[0,
)在区间[0, ![]() ]上是增函数;
]上是增函数;
③函数f(x)=cos(2x+ ![]() )的一个对称中心为(﹣
)的一个对称中心为(﹣ ![]() ,0)
,0)
④记min{a,b}= ![]() ,若函数f(x)=min{sinx,cosx},则f(x)的值域为[﹣1,
,若函数f(x)=min{sinx,cosx},则f(x)的值域为[﹣1, ![]() ].
].
其是叙述正确的是(请填上序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
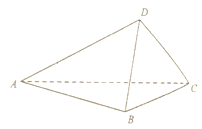
【题目】如图所示,在![]() 中,斜边
中,斜边![]() ,将
,将![]() 沿直线
沿直线![]() 旋转得到
旋转得到![]() ,设二面角
,设二面角![]() 的大小为
的大小为![]() .
.
(1)取![]() 的中点
的中点![]() ,过点
,过点![]() 的平面与
的平面与![]() 分别交于点
分别交于点![]() ,当平面
,当平面![]() 平面
平面![]() 时,求
时,求![]() 的长(2)当
的长(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.“x<﹣1”是“x2﹣x﹣2>0”的必要不充分条件
B.“P且Q”为假,则P假且 Q假
C.命题“ax2﹣2ax+3>0恒成立”是真命题,则实数a的取值范围是0≤a<3
D.命题“若x2﹣3x+2=0,则x=2”的否命题为“若x2﹣3x+2=0,则x≠2”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 
A.f(x)的图象关于直线x=﹣ ![]() 对称
对称
B.函数f(x)在[﹣ ![]() ,0]上单调递增
,0]上单调递增
C.f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
D.将函数y=2sin(2x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位得到f(x)的图象
个单位得到f(x)的图象
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com