
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 
A.f(x)的图象关于直线x=﹣ ![]() 对称
对称
B.函数f(x)在[﹣ ![]() ,0]上单调递增
,0]上单调递增
C.f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
D.将函数y=2sin(2x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位得到f(x)的图象
个单位得到f(x)的图象
【答案】B
【解析】解:由题设图象知,周期T=4( ![]() )=π, ∴ω=
)=π, ∴ω= ![]() =2.
=2.
∵点( ![]() ,0)在函数图象上,
,0)在函数图象上,
∴Asin(2× ![]() +φ)=0,即sin(
+φ)=0,即sin( ![]() +φ)=0.
+φ)=0.
又∵ ![]() <φ<
<φ< ![]() ,
,
∴ ![]() <
< ![]() +φ<
+φ< ![]() ,从而
,从而 ![]() +φ=π,即φ=
+φ=π,即φ= ![]() .
.
又点( ![]() ,2)在函数图象上,
,2)在函数图象上,
∴Asin ![]() =2,∴A=2.
=2,∴A=2.
故函数f(x)的解析式为f(x)=2sin(2x+ ![]() ).
).
对称轴方程为:2x+ ![]() =
= ![]() ,(k∈Z),经考查A不对.
,(k∈Z),经考查A不对.
由 ![]() 可知,函数f(x)在[﹣
可知,函数f(x)在[﹣ ![]() ,0]上单调递增,故B对.
,0]上单调递增,故B对.
当x=- ![]() 时,f(﹣
时,f(﹣ ![]() )=﹣2,故图象不是关于点(﹣
)=﹣2,故图象不是关于点(﹣ ![]() ,0)对称,故C不对.
,0)对称,故C不对.
函数y=2sin(2x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位得到y′=2sin(2x+
个单位得到y′=2sin(2x+ ![]() ﹣
﹣ ![]() )=2sin(2x+
)=2sin(2x+ ![]() ),没有得到f(x)的图象,故D不对.
),没有得到f(x)的图象,故D不对.
故选B.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
(1)求椭圆的标准方程
(2)设直线l:y=kx+1与椭圆C相交于P,Q两点,是否存在这样的实数k,使得以PQ为直径的圆过原点,若存在,请求出k的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
.
(Ⅰ)求证:平面PAM⊥平面PDM;
(Ⅱ)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.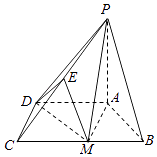
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】F1 , F2分别是双曲线x2﹣ ![]() =1(b>0)的左、右焦点,过F2的直线l与双曲线的左右两支分别交于A,B两点,若△ABF1是等边三角形,则该双曲线的虚轴长为( )
=1(b>0)的左、右焦点,过F2的直线l与双曲线的左右两支分别交于A,B两点,若△ABF1是等边三角形,则该双曲线的虚轴长为( )
A.2 ![]()
B.2 ![]()
C.![]()
D.4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修 4-4]参数方程与极坐标系
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线
轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线 ![]() :
: ![]() .
.
(Ⅰ)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
[选修 4-5]不等式选讲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a. 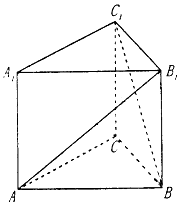
(1)求证:AB1⊥BC1;
(2)求二面角B﹣AB1﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),满足f(1)=0,且在(0,+∞)上单调递增,则xf(x)>0的解集为( )
A.{x|x<﹣1或x>1}
B.{x|0<x<1或﹣1<x<0}
C.{x|0<x<1或x<﹣1}
D.{x|﹣1<x<0或x>1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com