
【题目】五面体![]() 中,
中,![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
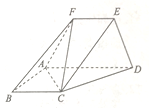
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1) 连接![]() ,取
,取![]() 中点为
中点为![]() ,则
,则![]() ,可得
,可得![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,由题意平面
,由题意平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,![]() 平面
平面![]() ,
,![]() 又
又![]() ,
,![]() ,可得结论;
,可得结论;
(2)以![]() 为原点,
为原点,![]() 分别为轴
分别为轴![]() ,
,![]() 轴正方向,在平面
轴正方向,在平面![]() 内,过点
内,过点![]() 且与
且与![]() 垂直的直线为
垂直的直线为![]() 轴建立如图所示的空间直角坐标系,由题意可知
轴建立如图所示的空间直角坐标系,由题意可知![]() . 可得
. 可得 ,
,![]() ,
,![]() .平面
.平面![]() 的一个法向量为
的一个法向量为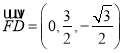 ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,求
,求![]() 的值后用
的值后用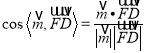 公式,可得答案.
公式,可得答案.
解:(1)连接![]() ,取
,取![]() 中点为
中点为![]() ,则
,则![]() ,
,
![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() .
.
![]() 为等边三角形,
为等边三角形,![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
![]() 平面
平面![]() ,
,
![]() .
.
又![]() ,
,![]()
![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 分别为轴
分别为轴![]() ,
,![]() 轴正方向,在平面
轴正方向,在平面![]() 内,过点
内,过点![]() 且与
且与![]() 垂直的直线为
垂直的直线为![]() 轴建立如图所示的空间直角坐标系,由题意可知
轴建立如图所示的空间直角坐标系,由题意可知![]() .
.

则 ,
,![]() ,
,![]() .
.
由(1)知,平面![]() 的一个法向量为
的一个法向量为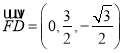 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则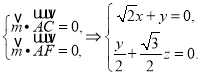
取![]() ,得
,得![]() ,
,
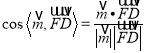
 ,
,
![]() 结合图形可知二面角
结合图形可知二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一片森林原来面积为![]() ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的![]() ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的![]() .
.
(1)到今年为止,该森林已砍伐了多少年?
(2)今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.
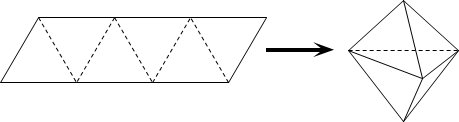
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一工厂计划生产某种当地政府控制产量的特殊产品,月固定成本为1万元,设此工厂一个月内生产该特殊产品![]() 万件并全部销售完.根据当地政府要求产量
万件并全部销售完.根据当地政府要求产量![]() 满足
满足![]() ,每生产
,每生产![]() 件需要再投入
件需要再投入![]() 万元,每1万件的销售收入为
万元,每1万件的销售收入为![]() (万元),且每生产1万件产品政府给予补助
(万元),且每生产1万件产品政府给予补助![]() (万元).(注:月利润=月销售收入+月政府补助-月总成本).
(万元).(注:月利润=月销售收入+月政府补助-月总成本).
(1)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(2)求该工厂在生产这种特殊产品中所获得的月利润最大值(万元)及此时的月生产量(万件)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有![]() 名学生,其中男生
名学生,其中男生![]() 人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了
人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了![]() 名学生进行调查,月消费金额分布在
名学生进行调查,月消费金额分布在![]() 之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
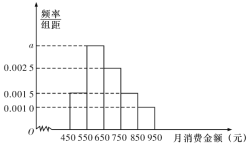
将月消费金额不低于![]() 元的学生称为“高消费群”.
元的学生称为“高消费群”.
(1)求![]() 的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从月消费金额落在![]() ,
,![]() 内的两组学生中抽取
内的两组学生中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,记被抽取的
人,记被抽取的![]() 名学生中属于“高消费群”的学生人数为随机变量
名学生中属于“高消费群”的学生人数为随机变量![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
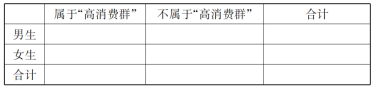
(3)若样本中属于“高消费群”的女生有![]() 人,完成下列
人,完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该校学生属于“高消费群”与“性别”有关?
的把握认为该校学生属于“高消费群”与“性别”有关?
(参考公式: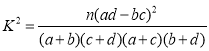 ,其中
,其中![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() ,E,F分别为棱PB,PC的中点,过E,F的平面分别与棱AB,AC相交于点D,G,给出以下四个结论:
,E,F分别为棱PB,PC的中点,过E,F的平面分别与棱AB,AC相交于点D,G,给出以下四个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则以上正确结论的个数是
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com