
若等差数列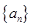 的首项为
的首项为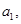 公差为
公差为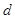 ,前
,前 项的和为
项的和为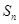 ,则数列
,则数列 为等差数列,且通项为
为等差数列,且通项为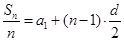 .类似地,请完成下列命题:若各项均为正数的等比数列
.类似地,请完成下列命题:若各项均为正数的等比数列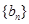 的首项为
的首项为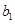 ,公比为
,公比为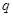 ,前
,前 项的积为
项的积为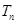 ,则 .
,则 .
科目:高中数学 来源: 题型:填空题
已知点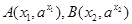 是函数
是函数 的图象上任意不同两点,依据图象可知,线段AB总是位于A、B两点之间函数图象的上方,因此有结论
的图象上任意不同两点,依据图象可知,线段AB总是位于A、B两点之间函数图象的上方,因此有结论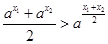 成立.运用类比思想方法可知,若点
成立.运用类比思想方法可知,若点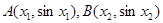 是函数
是函数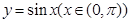 的图象上任意不同两点,则类似地有_________________成立.
的图象上任意不同两点,则类似地有_________________成立.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ;类比到空间,有两个棱长均为
;类比到空间,有两个棱长均为 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .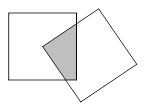
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若三角形内切圆的半径为r,三边长为 ,则三角形的面积
,则三角形的面积 ,根据类比思想,若四面体内切球半径为R,四个面的面积为S1、S2、S3、S4,则四面体的体积V= .
,根据类比思想,若四面体内切球半径为R,四个面的面积为S1、S2、S3、S4,则四面体的体积V= .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下面几种推理是合情推理的是 。(填序号)
①由圆的性质类比出球的性质;
②由直角三角形、等腰三角形、等边三角形的内角和是1800,归纳得出所有三角形的内角和为1800;
③小王某次考试成绩是100分,由此推出全班同学的成绩都是100分;
④三角形的内角和是1800,四边形内角和是3600,五边形的内角和是5400,由此得凸n边形的内角和是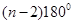 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
用数学归纳法证明“12+22+32+…+n2=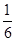 n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com