
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() 使得
使得![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)首先求得导函数的解析式,然后结合函数的定义域和导函数的符号分类讨论即可确定函数的单调区间;
(Ⅱ)首先求得函数![]() 的最大值,然后进行等价转化,结合(Ⅰ)中的结果分类讨论即可确定
的最大值,然后进行等价转化,结合(Ⅰ)中的结果分类讨论即可确定![]() 的取值范围.
的取值范围.
(Ⅰ)![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,
,
在区间![]() 上,
上,![]() ;在区间
;在区间![]() 上
上![]() ,
,
故![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
②当![]() 时,
时,![]() ,
,
在区间![]() 和
和![]() 上,
上,![]() ;在区间
;在区间![]() 上
上![]() ,
,
故![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
③当![]() 时,
时,![]() ,故
,故![]() 的单调递增区间是
的单调递增区间是![]() .
.
④当![]() 时,
时,![]() ,在区间
,在区间![]() 和
和![]() 上,
上,![]() ;区间
;区间![]() 上
上![]() ,
,
故![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,![]() 为增函数,
为增函数,
由已知,![]() .据此可得
.据此可得![]() .
.
由(Ⅰ)可知,
①当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
故![]()
![]() ,
,
所以,![]() ,解得
,解得![]() ,故
,故![]() .
.
②当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() .
.
由![]() 可知
可知![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,
,![]() ,
,
综上所述,![]() .
.


科目:高中数学 来源: 题型:
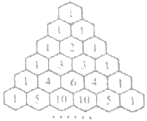
【题目】如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列前21项的和为_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-![]() x3+2x2+2x,若存在满足0≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
x3+2x2+2x,若存在满足0≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
A. [6,+∞)B. (-∞,2]
C. [2,6]D. [5,6]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,底面ABCD四边长为1的菱形,∠ABC=![]() ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
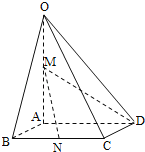
(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小;
(3)求点B到平面OCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com