
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ,
, ![]() (2)①详见解析,②不存在
(2)①详见解析,②不存在
【解析】试题分析:(1)数列![]() 递推关系式是一个分段函数,可通过分段点进行连接:
递推关系式是一个分段函数,可通过分段点进行连接: ![]() ,
, ![]() ,
, ![]() ,根据对勾函数得
,根据对勾函数得![]() ,或
,或![]() ,从而有
,从而有![]() (2)①当
(2)①当![]() 时,数列
时,数列![]() 是一个等差数列,易得
是一个等差数列,易得![]() ,从而
,从而![]() ,令
,令![]() ,得
,得![]() .问题转化为证明
.问题转化为证明![]() 有满足条件
有满足条件![]() 解,易求得
解,易求得![]() ②
②![]() ∴
∴![]()
![]() ,问题转化为是否存在三个不同的整数
,问题转化为是否存在三个不同的整数![]() (
(![]() ),使得
),使得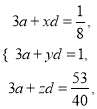 消去a,d得
消去a,d得![]() ,由于
,由于![]() ,所以无解
,所以无解
试题解析:(1)当![]() 时,
时,
![]() ,
, ![]() ,
, ![]() . 2分
. 2分
因为![]() ,
, ![]() ,或
,或![]() ,
,
所以![]() . 4分
. 4分
(2)①由题意![]() ,
, ![]() ,
, ![]() . 6分
. 6分
令![]() ,得
,得![]() .
.
因为![]() ,
, ![]() ,
,
所以令![]() ,则
,则![]() . 8分
. 8分
②不存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 同时属于
同时属于![]() . 9分
. 9分
假设存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 同时属于
同时属于![]() .
.
![]() ,∴
,∴![]() ,
,
从而![]() . 11分
. 11分
因为![]() ,
, ![]() ,
, ![]() 同时属于
同时属于![]() ,所以存在三个不同的整数
,所以存在三个不同的整数![]() (
(![]() ),
),
使得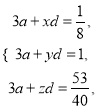 从而
从而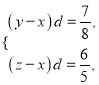
则![]() . 13分
. 13分
因为![]() 与
与![]() 互质,且
互质,且![]() 与
与![]() 为整数,
为整数,
所以![]() ,但
,但![]() ,矛盾.
,矛盾.
所以不存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() . 16分
. 16分


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn= ![]() (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上(异于端点),设a,b,c,p均为非零实数,直线BP,CP分别交AC,AB于点E,F,一同学已正确算的OE的方程:( ![]() ﹣
﹣ ![]() )x+(
)x+( ![]() ﹣
﹣ ![]() )y=0,请你求OF的方程:()x+(
)y=0,请你求OF的方程:()x+( ![]() ﹣
﹣ ![]() )y=0.
)y=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的方程ax2+2x+1=0至少有一个负根,q:a≤1,则¬p是¬q的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题. 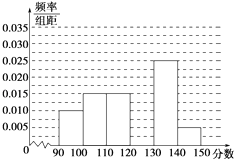
(1)从该校高三模拟考试的成绩中随机抽取一份,利用随机事件频率估计概率,求数学分数恰在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,连结
的中点,连结![]() .求证:
.求证:

(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() ;
;
(2)设 ![]() =(0,1),若
=(0,1),若 ![]() +
+ ![]() =
= ![]() ,求α,β的值.
,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{![]() }中,
}中,![]() ,且
,且![]() 对任意正整数都成立,数列{
对任意正整数都成立,数列{![]() }的前n项和为Sn。
}的前n项和为Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在实数k,使数列{![]() }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com