
【题目】在平面直角坐标系中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上(异于端点),设a,b,c,p均为非零实数,直线BP,CP分别交AC,AB于点E,F,一同学已正确算的OE的方程:( ![]() ﹣
﹣ ![]() )x+(
)x+( ![]() ﹣
﹣ ![]() )y=0,请你求OF的方程:()x+(
)y=0,请你求OF的方程:()x+( ![]() ﹣
﹣ ![]() )y=0.
)y=0.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗) 
(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(2)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题的是( )
A.已知f(x)=sin2x+ ![]() ,则f(x)的最小值是2
,则f(x)的最小值是2 ![]()
B.已知数列{an}的通项公式为an=n+ ![]() ,则{an}的最小项为2
,则{an}的最小项为2 ![]()
C.已知实数x,y满足x+y=2,则xy的最大值是1
D.已知实数x,y满足xy=1,则x+y的最小值是2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1 , 连接AP交棱CC1于点D.以A1为坐标原点建立空间直角坐标系,如图所示.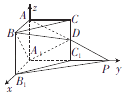
(1)写出A1、B、B1、C、D、P的坐标;
(2)求异面直线A1B与PB1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,直线y=x﹣8与此抛物线交于A、B两点,与x轴交于点C,O为坐标原点,若 ![]() =3
=3 ![]() .
.
(1)求此抛物线的方程;
(2)求证:OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)求直线AB与平面CBF所成角的大小;
(Ⅲ)当AD的长为何值时,平面DFC与平面FCB所成的锐二面角的大小为60°?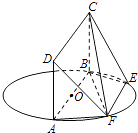
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获纯利多少元?
已知: ![]() x
x ![]() =280,
=280, ![]() y
y ![]() =45309,
=45309, ![]() xiyi=3487,
xiyi=3487, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com