
【题目】一个多边形剪一刀(截痕不过多边形的顶点)分割为![]() 个多边形,再将其中一个多边形剪一刀(截痕不过多边形的顶点)又分割出一个多边形,……如此下去。如果从一个正方形开始,要剪出一个三角形,一个四边形,一个五边形,……一个
个多边形,再将其中一个多边形剪一刀(截痕不过多边形的顶点)又分割出一个多边形,……如此下去。如果从一个正方形开始,要剪出一个三角形,一个四边形,一个五边形,……一个![]() 边形,那么,所需要剪的最少刀数为________。
边形,那么,所需要剪的最少刀数为________。
【答案】![]()
【解析】
设共剪了![]() 刀.由于每剪一刀增加一个多边形,从而,共有
刀.由于每剪一刀增加一个多边形,从而,共有![]() 个多边形,除一个三角形,一个四边形,一个五边形,………一个
个多边形,除一个三角形,一个四边形,一个五边形,………一个![]() 边形外,还有
边形外,还有![]() 个多边形.
个多边形.
考察这些多边形的边数的总和![]() ,则
,则![]() .
.
又每剪一刀增加![]() 条边(原多边形有两条边被一分为二,且截痕为两条新增的边),于是,
条边(原多边形有两条边被一分为二,且截痕为两条新增的边),于是,![]() .
.
所以,![]() ,即
,即![]() .
.
另一方面,先将正方形剪一刀剪成一个三角形和一个五边形,再将其中的五边形剪一刀剪成一个四边形和一个五边形,又将其中的五边形剪一刀剪成一个四边形和一个五边形,然后将其中的四边形剪一刀剪成一个三角形和一个五边形,再将其中的五边形剪一刀剪成一个三角形和一个六边形,至此,共剪了五刀,剪出了两个三角形、一个四边形、一个五边形、一个六边形.现在对其中一个三角形操作,每剪一刀都剪出一个三角形,剪四刀剪成一个七边形和若干个三角形,以后都选择一个三角形,剪![]() 刀剪成一个
刀剪成一个![]() 边形和若干个三角形.这样一共剪了
边形和若干个三角形.这样一共剪了![]() 刀.
刀.
所以,![]() 的最小值为
的最小值为![]() .
.
故答案为:![]()


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(1)试判断数列![]() 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出通项公式
是等比数列,并求出通项公式![]() ;
;
(3)在数列![]() 中依据某种顺序从左至右取出其中的项
中依据某种顺序从左至右取出其中的项![]() ,…,把这些项重新组成一个新数列
,…,把这些项重新组成一个新数列![]() ,….若数列
,….若数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的无穷等比数列,且数列
的无穷等比数列,且数列![]() 各项的和为
各项的和为![]() ,求正整数
,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价为每天180元时,房间会全部住满;房间单价增加10元,就会有一个房间空闲,如果游客居住房间,宾馆每间每天需花费20元的各种维护费用.房间定价多少时,宾馆利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才.对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
| 一般 | 良好 | 优秀 |
一般 |
|
|
|
良好 |
|
|
|
优秀 |
|
|
|
例如表中运动协调能力良好且逻辑思维能力一般的学生是![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)从运动协调能力为优秀的学生中任意抽取![]() 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自古以来“民以食为天”,餐饮业作为我国第三产业中的一个支柱产业,一直在社会发展与人民生活中发挥着重要作用.某机构统计了2010~2016年餐饮收入的情况,得到下面的条形图,则下面结论中不正确的是( )

A. 2010~2016年全国餐饮收入逐年增加
B. 2016年全国餐饮收入比2010年翻了一番以上
C. 2010~2016年全国餐饮收入同比增量最多的是2015年
D. 2010~2016年全国餐饮收入同比增量超过3000亿元的年份有3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设四边形![]() 为矩形,点
为矩形,点![]() 为平面
为平面![]() 外一点,且
外一点,且![]() 平面
平面![]() ,若
,若![]() ,
,![]() .
.
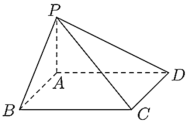
(1)求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若点![]() 是
是![]() 的中点,在
的中点,在![]() 内确定一点
内确定一点![]() ,使
,使![]() 的值最小,并求此时
的值最小,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点在
的两焦点在![]() 轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为
轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆的方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设锐角![]() 的外接圆的半径为
的外接圆的半径为![]() ,在
,在![]() 内取外接圆的同心圆
内取外接圆的同心圆![]() ,其半径为
,其半径为![]()
![]() ,从圆
,从圆![]() 上任取一点
上任取一点![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
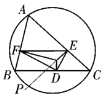
(1)求证:![]() 的面积为定值;
的面积为定值;
(2)猜想:当![]() 为任意三角形、同心圆
为任意三角形、同心圆![]() 为任意同心圆时,结论是否成立(不要求证明)?
为任意同心圆时,结论是否成立(不要求证明)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com