
【题目】某电子公司新开发一电子产品,该电子产品的一个系统G有3个电子元件组成,各个电子元件能否正常工作的概率均为![]() ,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
(1)求系统不需要维修的概率;
(2)该电子产品共由3个系统G组成,设E为电子产品需要维修的系统所需的费用,求![]() 的分布列与期望;
的分布列与期望;
(3)为提高G系统正常工作概率,在系统内增加两个功能完全一样的其他品牌的电子元件,每个新元件正常工作的概率均为![]() ,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:
,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:![]() 满足什么条件时,可以提高整个G系统的正常工作概率?
满足什么条件时,可以提高整个G系统的正常工作概率?
【答案】(1)![]() ;(2)见解析;(3) 当
;(2)见解析;(3) 当![]() 时,可以提高整个
时,可以提高整个![]() 系统的正常工作概率.
系统的正常工作概率.
【解析】
(1)由条件,利用独立重复试验成功的次数对应的概率公式以及概率加法公式求得系统不需要维修的概率;
(2)设![]() 为维修维修的系统的个数,根据题意可得
为维修维修的系统的个数,根据题意可得![]() ,从而得到
,从而得到![]() ,利用公式写出分布列,并求得期望;
,利用公式写出分布列,并求得期望;
(3)根据题意,当系统![]() 有5个电子元件时,分析得出系统正常工作对应的情况,分类得出结果,求得相应的概率,根据题意列出式子,最后求得结果.
有5个电子元件时,分析得出系统正常工作对应的情况,分类得出结果,求得相应的概率,根据题意列出式子,最后求得结果.
(1)系统不需要维修的概率为![]() .
.
(2)设![]() 为维修维修的系统的个数,则
为维修维修的系统的个数,则![]() ,且
,且![]() ,
,
所以![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 500 | 1000 | 1500 |
|
|
|
|
|
所以![]() 的期望为
的期望为![]() .
.
(3)当系统![]() 有5个电子元件时,
有5个电子元件时,
原来3个电子元件中至少有1个元件正常工作,![]() 系统的才正常工作.
系统的才正常工作.
若前3个电子元件中有1个正常工作,同时新增的两个必须都正常工作,
则概率为![]() ;
;
若前3个电子元件中有两个正常工作,
同时新增的两个至少有1个正常工作,
则概率为![]() ;
;
若前3个电子元件中3个都正常工作,则不管新增两个元件能否正常工作,
系统![]() 均能正常工作,则概率为
均能正常工作,则概率为![]() .
.
所以新增两个元件后系统![]() 能正常工作的概率为
能正常工作的概率为![]() ,
,
于是由![]() 知,当
知,当![]() 时,即
时,即![]() 时,
时,
可以提高整个![]() 系统的正常工作概率.
系统的正常工作概率.


科目:高中数学 来源: 题型:
【题目】定义:首项为![]() 且公比为正数的等比数列为“
且公比为正数的等比数列为“![]() 数列”.
数列”.
(Ⅰ)已知等比数列![]() (
(![]() )满足:
)满足:![]() ,
,![]() ,判断数列
,判断数列![]() 是否为“
是否为“![]() 数列”;
数列”;
(Ⅱ)设![]() 为正整数,若存在“
为正整数,若存在“![]() 数列”
数列”![]() (
(![]() ),
),![]() 对任意不大于
对任意不大于![]() 的正整数
的正整数![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆右焦点
,过椭圆右焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当直线![]() 与
与![]() 轴不垂直时,在
轴不垂直时,在![]() 轴上是否存在一点
轴上是否存在一点![]() (异于点
(异于点![]() ),使
),使![]() 轴上任意点到直线
轴上任意点到直线![]() ,
,![]() 的距离均相等?若存在,求
的距离均相等?若存在,求![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
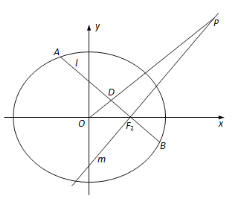
【题目】在平面直角坐标系![]() 中,已知中心在坐标原点,焦点在坐标轴上的椭圆
中,已知中心在坐标原点,焦点在坐标轴上的椭圆![]() 的右焦点为
的右焦点为![]() ,且离心率
,且离心率![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,过
的中点,过![]() 作直线
作直线![]() 的垂线
的垂线![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)证明:点![]() 在一条定直线上;
在一条定直线上;
(3)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 两点分别在线段
两点分别在线段![]() ,
,![]() 上运动,且
上运动,且![]() .将三角形
.将三角形![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.
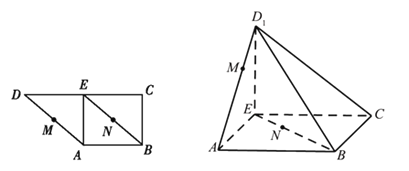
(1)判断直线![]() 与平面
与平面![]() 的位置关系并证明;
的位置关系并证明;
(2)证明:![]() 的长度最短时,
的长度最短时,![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中点;
的中点;
(3)当![]() 的长度最短时,求平面
的长度最短时,求平面![]() 与平面
与平面![]() 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C的方程;
(2)若点A、B为椭圆C的左右顶点,直线![]() 与x轴交于点D,点P是椭圆C上异于A、B的动点,直线AP、BP分别交直线
与x轴交于点D,点P是椭圆C上异于A、B的动点,直线AP、BP分别交直线![]() 于E、F两点,当点P在椭圆C上运动时,
于E、F两点,当点P在椭圆C上运动时,![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com